题目内容
【题目】一个袋子里装有7个球,其中有红球4个.白球3个.这些球除颜色外全相同.
(1)若一次从袋中取出3个球,取出的球颜色不完全相同的概率;
(2)若一次从袋中取出3个球.其中若取到红球得0分,取到白球得1分,记随机变量![]() 为取出的三个小球得分之和,求
为取出的三个小球得分之和,求![]() 的分布列,并求其数学期望.
的分布列,并求其数学期望.
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() .
.
【解析】
(1)根据组合知识可知一次从袋中取出3个球的基本事件总数为![]() ,分类可知取出的球颜色不完全相同的取法总数,利用古典概型求解即可;
,分类可知取出的球颜色不完全相同的取法总数,利用古典概型求解即可;
(2)![]() 的可能取值为0,1,2,3,利用古典概型分别计算其概率,列出分布列,求期望即可.
的可能取值为0,1,2,3,利用古典概型分别计算其概率,列出分布列,求期望即可.
(1)一次从袋中取出3个球的基本事件总数为![]() 种.
种.
设“取出的球颜色不完全相同”为事件A,共有两大类,
两红一白:![]() ,两白一红:
,两白一红:![]() ,
,
![]() .
.
(2)3个红球得0分:![]() ;
;
2红1白得1分:![]() ;
;
1红2白得2分:![]() ;
;
3个白球得3分:![]() ;
;
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.

练习册系列答案
相关题目
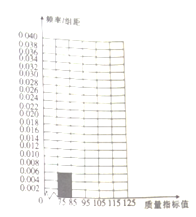
【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,现用一种新配方做试验,生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
质量指标值 |
|
|
|
|
|
频数 | 6 | 26 | 38 | 22 | 8 |
(1)将答题卡上列出的这些数据的频率分布表填写完整,并补齐频率分布直方图;
(2)估计这种产品质量指标值的平均值(同一组中的数据用该组区间的中点值作代表)与中位数(结果精确到0.1).
质量指标值分组 | 频数 | 频率 |
| 6 | 0.06 |
| ||
| ||
| ||
| ||
合计 | 100 | 1 |