题目内容
【题目】如图,已知椭圆![]() 上顶点为A,右焦点为F,直线
上顶点为A,右焦点为F,直线![]() 与圆
与圆![]() 相切,其中
相切,其中![]() .
.
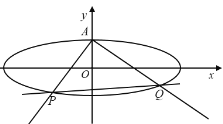
(1)求椭圆的方程;
(2)不过点A的动直线l与椭圆C相交于P,Q两点,且![]() ,证明:动直线l过定点,并且求出该定点坐标.
,证明:动直线l过定点,并且求出该定点坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)确定圆M的圆心与半径,利用直线AF与圆M相切关系,根据点到直线的距离公式构建方程,求得a,即可表示方程;
(2)设直线AP的方程为![]() ,则直线AQ的方程为
,则直线AQ的方程为![]() ,分别于椭圆联立方程求得交点P、Q的坐标,即可表示直线l的方程,得答案.
,分别于椭圆联立方程求得交点P、Q的坐标,即可表示直线l的方程,得答案.
(1)由题可知,![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,即
,即![]()
因为直线![]() 与圆
与圆![]() 相切,该圆的圆心为
相切,该圆的圆心为![]()
则
故椭圆的标准方程为![]()
(2)因为不过点A的动直线l与椭圆C相交于P,Q两点,且![]() ,即直线AP与坐标轴不垂直也不平行
,即直线AP与坐标轴不垂直也不平行
由![]() 可设直线AP的方程为
可设直线AP的方程为![]() ,则直线AQ的方程为
,则直线AQ的方程为![]()
联立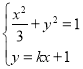 ,消去y并整理得
,消去y并整理得![]() ,解得
,解得![]() 或
或![]() ,
,
因此点P的坐标为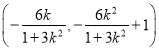 ,即
,即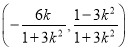
将上式中的k换成![]() ,得点Q
,得点Q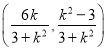
所以直线l的斜率为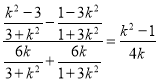 ,
,
即直线l的方程为![]() ,
,
化简并整理得![]() ,
,
故直线l恒过定点![]()

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】为了了解某市民众对某项公共政策的态度,在该市随机抽取了50名市民进行调查,作出他们的月收入(单位:百元,范围:![]() )的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
)的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:

月收入 | 赞成的人数 |
| 4 |
| 8 |
| 12 |
| 5 |
| 2 |
| 2 |
(1)求月收入在![]() 内的频率,补全频率分布直方图,并在图中标出相应纵坐标;
内的频率,补全频率分布直方图,并在图中标出相应纵坐标;
(2)若从月收入在![]() 内的被调查者中随机选取2人,求这2人对该项政策都不赞成的概率.
内的被调查者中随机选取2人,求这2人对该项政策都不赞成的概率.