��Ŀ����
��֪����f(x)=6x�C6x2���躯��g1(x)=f(x), g2(x)=f��g1(x)��, g3(x)=f ��g2(x)��,��gn(x)=f��gn�C1(x)��,��
��1����֤:�������һ��ʵ��x0������g1(x0)=x0����ô��һ��n��N��gn(x0)=x0��������
��2����ʵ��x0����gn(x0)=x0�����x0Ϊ�ȶ������㣬�����������Щ�ȶ������㣻
��3��������A=���C��,0��,��������x��A����g1(x)=f(x)=a��0, g2(x)=f��g1(x)��=f(0)��0��
��n��2ʱ��gn(x)��0 �����Ƿ��������B��A��B��
�����Ƿ��������B��A��B�� ������������������ʵ��x��ֻҪn��2������gn(x)��0.
������������������ʵ��x��ֻҪn��2������gn(x)��0.
��1����֤:�������һ��ʵ��x0������g1(x0)=x0����ô��һ��n��N��gn(x0)=x0��������
��2����ʵ��x0����gn(x0)=x0�����x0Ϊ�ȶ������㣬�����������Щ�ȶ������㣻
��3��������A=���C��,0��,��������x��A����g1(x)=f(x)=a��0, g2(x)=f��g1(x)��=f(0)��0��
��n��2ʱ��gn(x)��0
 �����Ƿ��������B��A��B��
�����Ƿ��������B��A��B�� ������������������ʵ��x��ֻҪn��2������gn(x)��0.
������������������ʵ��x��ֻҪn��2������gn(x)��0. (1)֤���ԣ� (2)�ȶ�������Ϊ0��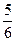 ��3��ֻҪn��2,n��N������gn(x)��0
��3��ֻҪn��2,n��N������gn(x)��0
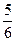 ��3��ֻҪn��2,n��N������gn(x)��0
��3��ֻҪn��2,n��N������gn(x)��0(1)֤��: ��n=1ʱ��g1(x0)=x0��Ȼ������
��n=kʱ����gk(x0)=x0(k��N)������
��gk+1(x0)=f��gk(x0)��=f(x0)=g1(x0)=x0
��n=k+1ʱ���������.
���һ��n��N,��g1(x0)=x0����gn(x0)=x0.
��2����:�ɣ�1��֪���ȶ�������x0ֻ������f(x0)=x0
��f(x0)=x0����6x0�C6x02=x0,��x0=0��x0=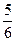
���ȶ�������Ϊ0��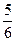 .
.
(3)��:��f(x)��0����6x�C6x2��0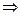 x��0��x��1.
x��0��x��1.
��gn(x)��0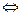 f��gn�C1(x)�ݣ�0
f��gn�C1(x)�ݣ�0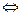 gn�C1(x)��0��gn�C1(x)��1
gn�C1(x)��0��gn�C1(x)��1
Ҫʹһ��n��N,n��2������gn(x)��0��������g1(x)��0��g1(x)��1.
��g1(x)��0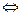 6x�C6x2��0
6x�C6x2��0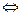 x��0��x��1
x��0��x��1
��g1(x)��0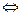 6x�C6x2��1
6x�C6x2��1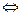
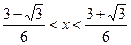
�ʶ�������(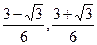 )��(1,+��)�ڵ�����ʵ��x,
)��(1,+��)�ڵ�����ʵ��x,
ֻҪn��2,n��N������gn(x)��0.
��n=kʱ����gk(x0)=x0(k��N)������
��gk+1(x0)=f��gk(x0)��=f(x0)=g1(x0)=x0
��n=k+1ʱ���������.
���һ��n��N,��g1(x0)=x0����gn(x0)=x0.
��2����:�ɣ�1��֪���ȶ�������x0ֻ������f(x0)=x0
��f(x0)=x0����6x0�C6x02=x0,��x0=0��x0=
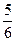
���ȶ�������Ϊ0��
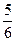 .
.(3)��:��f(x)��0����6x�C6x2��0
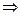 x��0��x��1.
x��0��x��1. ��gn(x)��0
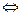 f��gn�C1(x)�ݣ�0
f��gn�C1(x)�ݣ�0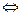 gn�C1(x)��0��gn�C1(x)��1
gn�C1(x)��0��gn�C1(x)��1Ҫʹһ��n��N,n��2������gn(x)��0��������g1(x)��0��g1(x)��1.
��g1(x)��0
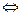 6x�C6x2��0
6x�C6x2��0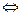 x��0��x��1
x��0��x��1��g1(x)��0
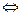 6x�C6x2��1
6x�C6x2��1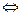
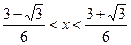
�ʶ�������(
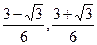 )��(1,+��)�ڵ�����ʵ��x,
)��(1,+��)�ڵ�����ʵ��x,ֻҪn��2,n��N������gn(x)��0.

��ϰ��ϵ�д�
 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
�����Ŀ
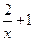 ��=lgx����f��x����
��=lgx����f��x����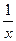 ��=3x����f��x��.
��=3x����f��x��.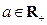 ��������
��������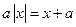 ������ʵ���⣬��ʵ��
������ʵ���⣬��ʵ��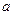 ��ȡֵ��Χ��
��ȡֵ��Χ��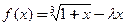 ������
������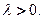
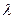 ��ȡֵ��Χ��ʹ�ú���
��ȡֵ��Χ��ʹ�ú���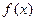 ��
��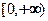 ���ǵ����ݼ�������
���ǵ����ݼ�������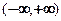 �ϣ�
�ϣ�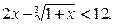
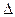 ABP���ΪS.��1������S=f(x)�Ľ���ʽ���������ֵ��2����f[f(3)]��ֵ��
ABP���ΪS.��1������S=f(x)�Ľ���ʽ���������ֵ��2����f[f(3)]��ֵ��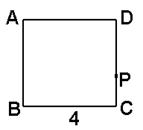
 �·ݣ���һ�¿��װͶ��ij�̳����ۣ�
�·ݣ���һ�¿��װͶ��ij�̳����ۣ� �ոÿ��װ�����۳�
�ոÿ��װ�����۳� �����ڶ����۳�
�����ڶ����۳� ��������������
��������������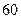 ����Ȼ��ÿ���۳��ļ����ֱ����
����Ȼ��ÿ���۳��ļ����ֱ����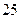 ����ֱ�����������ﵽ����ÿ�����۵ļ����ֱ�ݼ�
����ֱ�����������ﵽ����ÿ�����۵ļ����ֱ�ݼ�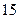 �������µ÷�װ�����۳�
�������µ÷�װ�����۳�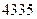 ����������
����������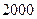 ��ʱ������Ͼ����У����������������½���������
��ʱ������Ͼ����У����������������½���������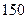 ��ʱ����������ʧ���ʸÿ��װ������������Ƿ�
��ʱ����������ʧ���ʸÿ��װ������������Ƿ�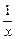 (x�ܣ�
(x�ܣ�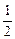 )��ֵ����( )
)��ֵ����( )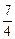
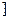
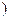
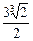 ,+��
,+��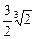 ��
��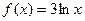 ����
����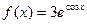 ����
����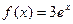 ����
����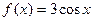 .�����
.���ж���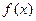 �������ڵ�����һ���Ա���
�������ڵ�����һ���Ա���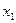 ������Ψһ���Ա���
������Ψһ���Ա���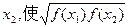 =3�����ĺ����ǣ� ��.
=3�����ĺ����ǣ� ��.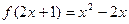 ����
����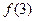 = .
= . 