题目内容
设函数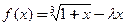 ,其中
,其中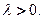
(1)求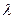 的取值范围,使得函数
的取值范围,使得函数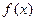 在
在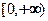 上是单调递减函数;
上是单调递减函数;
(2)此单调性能否扩展到整个定义域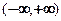 上?
上?
(3)求解不等式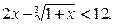
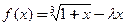 ,其中
,其中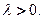
(1)求
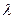 的取值范围,使得函数
的取值范围,使得函数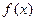 在
在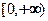 上是单调递减函数;
上是单调递减函数;(2)此单调性能否扩展到整个定义域
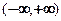 上?
上?(3)求解不等式
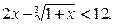
(1)只需要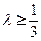 ,就能使
,就能使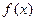 在
在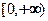 上是单调递减函数;
上是单调递减函数;
(2)此单调性不能扩展到整个定义域上(3)所求解集为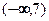
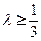 ,就能使
,就能使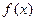 在
在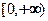 上是单调递减函数;
上是单调递减函数;(2)此单调性不能扩展到整个定义域上(3)所求解集为
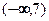
(1)设
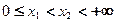 ,
,则

设
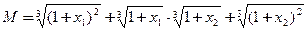 ,则显然
,则显然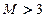 .
.∵
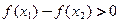 ,∴
,∴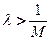 ,∵
,∵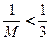 ,∴只需要
,∴只需要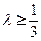 ,就能使
,就能使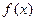 在
在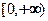 上是单调递减函数;
上是单调递减函数;(2)此单调性不能扩展到整个定义域上,这可由单调性定义说明之;
(3)构造函数
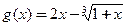 ,由(1)知当
,由(1)知当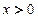 时,
时,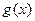 是单调递增函数。∵
是单调递增函数。∵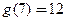 ,∴
,∴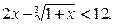
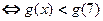 ,∴
,∴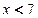 ,∴所求解集为
,∴所求解集为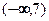 .
.
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
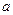 ,在今后
,在今后 年内,计划使产量平均每年比上一年增加
年内,计划使产量平均每年比上一年增加 ,写出产量随年数变化的函数解析式.
,写出产量随年数变化的函数解析式. 、
、 两地同时开出.已知
两地同时开出.已知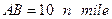 ,甲乙两船的速度分别是16 n mile/h和12 n mile/h,求多少时间后,两船距离最近,最近距离是多少?
,甲乙两船的速度分别是16 n mile/h和12 n mile/h,求多少时间后,两船距离最近,最近距离是多少?
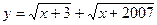 的正整数数对(x,y)( )
的正整数数对(x,y)( ) 试问是否存在区间B(A∩B≠
试问是否存在区间B(A∩B≠ ),对于区间内任意实数x,只要n≥2,都有gn(x)<0.
),对于区间内任意实数x,只要n≥2,都有gn(x)<0.  [f(x1)+f(x2)]与f(
[f(x1)+f(x2)]与f(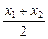 )的大小,并加以证明.
)的大小,并加以证明. 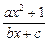 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<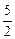 .试求函数f(x)的解析式
.试求函数f(x)的解析式