ЬтФПФкШн
ЁОЬтФПЁПЫЩНгаЙьЕчГЕЯюФПе§дкШчЛ№ШчнБЕФНјаажаЃЌЭЈГЕКѓНЋИјЪаУёГіааДјРДБуРћ. вбжЊФГЬѕЯпТЗЭЈГЕКѓЃЌЕчГЕЕФЗЂГЕЪБМфМфИє![]() ЃЈЕЅЮЛЃКЗжжгЃЉТњзу
ЃЈЕЅЮЛЃКЗжжгЃЉТњзу![]() . ОЪаГЁЕїбаВтЫуЃЌЕчГЕдиПЭСПгыЗЂГЕЪБМфМфИє
. ОЪаГЁЕїбаВтЫуЃЌЕчГЕдиПЭСПгыЗЂГЕЪБМфМфИє![]() ЯрЙиЃЌЕБ
ЯрЙиЃЌЕБ![]() ЪБЕчГЕЮЊТњдизДЬЌЃЌдиПЭСПЮЊ
ЪБЕчГЕЮЊТњдизДЬЌЃЌдиПЭСПЮЊ![]() ШЫЃЌЕБ
ШЫЃЌЕБ![]() ЪБЃЌдиПЭСПЛсМѕЩйЃЌМѕЩйЕФШЫЪ§гы
ЪБЃЌдиПЭСПЛсМѕЩйЃЌМѕЩйЕФШЫЪ§гы![]() ЕФЦНЗНГЩе§БШЃЌЧвЗЂГЕЪБМфМфИєЮЊ
ЕФЦНЗНГЩе§БШЃЌЧвЗЂГЕЪБМфМфИєЮЊ![]() ЗжжгЪБЕФдиПЭСПЮЊ
ЗжжгЪБЕФдиПЭСПЮЊ![]() ШЫ.МЧЕчГЕдиПЭСПЮЊ
ШЫ.МЧЕчГЕдиПЭСПЮЊ![]() .
.
ЃЈ1ЃЉЧѓ![]() ЕФБэДяЪНЃЌВЂЧѓЕБЗЂГЕЪБМфМфИєЮЊ
ЕФБэДяЪНЃЌВЂЧѓЕБЗЂГЕЪБМфМфИєЮЊ![]() ЗжжгЪБЃЌЕчГЕЕФдиПЭСПЃЛ
ЗжжгЪБЃЌЕчГЕЕФдиПЭСПЃЛ
ЃЈ2ЃЉШєИУЯпТЗУПЗжжгЕФОЛЪевцЮЊ![]() ЃЈдЊЃЉЃЌЮЪЕБЗЂГЕЪБМфМфИєЮЊЖрЩйЪБЃЌИУЯпТЗУПЗжжгЕФОЛЪевцзюДѓЃП
ЃЈдЊЃЉЃЌЮЪЕБЗЂГЕЪБМфМфИєЮЊЖрЩйЪБЃЌИУЯпТЗУПЗжжгЕФОЛЪевцзюДѓЃП
ЁОД№АИЁПЃЈ1ЃЉ ЃЌЕчГЕЕФдиПЭСПЮЊ
ЃЌЕчГЕЕФдиПЭСПЮЊ![]() ШЫЃЛЃЈ2ЃЉЕБЗЂГЕЪБМфМфИє
ШЫЃЛЃЈ2ЃЉЕБЗЂГЕЪБМфМфИє![]() ЗжжгЪБЃЌИУЯпТЗУПЗжжгЕФОЛЪевцзюДѓ.
ЗжжгЪБЃЌИУЯпТЗУПЗжжгЕФОЛЪевцзюДѓ.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтПЩЕУ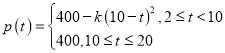 ЃЈ
ЃЈ![]() ЮЊГЃЪ§ЃЉЃЌНсКЯ
ЮЊГЃЪ§ЃЉЃЌНсКЯ![]() ПЩЧѓГі
ПЩЧѓГі![]() ЃЌНјЖјПЩЧѓГі
ЃЌНјЖјПЩЧѓГі![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉгЩЬтвтЕУГі![]() Йигк
Йигк![]() ЕФЗжЖЮКЏЪ§БэДяЪНЃЌРћгУЛљБОВЛЕШЪНКЭКЏЪ§ЕЅЕїадЗжЖЮЧѓГізюДѓжЕЃЌШЁСНепжаЕФзюДѓжЕМДПЩ.
ЕФЗжЖЮКЏЪ§БэДяЪНЃЌРћгУЛљБОВЛЕШЪНКЭКЏЪ§ЕЅЕїадЗжЖЮЧѓГізюДѓжЕЃЌШЁСНепжаЕФзюДѓжЕМДПЩ.
ЃЈ1ЃЉгЩЬтвтжЊ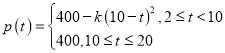 ЃЈ
ЃЈ![]() ЮЊГЃЪ§ ЃЉ
ЮЊГЃЪ§ ЃЉ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
Ыљвд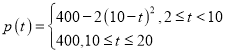 ЃЌЫљвд
ЃЌЫљвд![]() ЃЈШЫЃЉЃЌ
ЃЈШЫЃЉЃЌ
МДЕБЗЂГЕЪБМфМфИєЮЊ![]() ЗжжгЪБЃЌЕчГЕЕФдиПЭСПЮЊ
ЗжжгЪБЃЌЕчГЕЕФдиПЭСПЮЊ![]() ШЫЃЛ
ШЫЃЛ
ЃЈ2ЃЉгЩ![]() ПЩЕУ
ПЩЕУ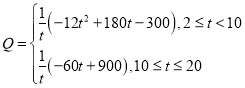 .
.
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЕБЧвНіЕБ![]() ЪБЕШКХГЩСЂЃЛ
ЪБЕШКХГЩСЂЃЛ
ЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕЅЕїЕнМѕЃЌдђ
ЕЅЕїЕнМѕЃЌдђ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЕШКХГЩСЂ
ЪБЕШКХГЩСЂ
вђДЫЃЌЕБЗЂГЕЪБМфМфИє![]() ЗжжгЪБЃЌИУЯпТЗУПЗжжгЕФОЛЪевцзюДѓЃЌзюДѓжЕЮЊ
ЗжжгЪБЃЌИУЯпТЗУПЗжжгЕФОЛЪевцзюДѓЃЌзюДѓжЕЮЊ![]() дЊ.
дЊ.

ЁОЬтФПЁПЖдгкЖЈвхгђЮЊRЕФКЏЪ§y=fЃЈxЃЉЃЌВПЗжxгыyЕФЖдгІЙиЯЕШчБэЃК
x | Љ2 | Љ1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 0 | 2 | 3 | 2 | 0 | Љ1 | 0 | 2 |
ЃЈ1ЃЉЧѓf{f[fЃЈ0ЃЉ]}ЃЛ
ЃЈ2ЃЉЪ§Са{xn}Тњзуx1=2ЃЌЧвЖдШЮвтnЁЪN*ЃЌЕуЃЈxnЃЌxn+1ЃЉЖМдкКЏЪ§y=fЃЈxЃЉЕФЭМЯѓЩЯЃЌЧѓx1+x2+Ё+x4nЃЛ
ЃЈ3ЃЉШєy=fЃЈxЃЉ=AsinЃЈІиx+ІеЃЉ+bЃЌЦфжаAЃО0ЃЌ0ЃМІиЃМІаЃЌ0ЃМІеЃМІаЃЌ0ЃМbЃМ3ЃЌЧѓДЫКЏЪ§ЕФНтЮіЪНЃЌВЂЧѓfЃЈ1ЃЉ+fЃЈ2ЃЉ+Ё+fЃЈ3nЃЉЃЈnЁЪN*ЃЉЃЎ
ЁОЬтФПЁПФГИпаЃНЁПЕЩчЭХЮЊЕїВщБОаЃДѓбЇЩњУПжмдЫЖЏЕФЪБГЄЃЌЫцЛњбЁШЁСЫ80УћбЇЩњЃЌЕїВщЫћУЧУПжмдЫЖЏЕФзмЪБГЄЃЈЕЅЮЛЃКаЁЪБЃЉЃЌАДее![]()
![]()
![]()
![]()
![]()
![]() ЙВ6зщНјааЭГМЦЃЌЕУЕНФаЩњЁЂХЎЩњУПжмдЫЖЏЕФЪБГЄЕФЭГМЦШчЯТЃЈБэ1ЁЂ2ЃЉЃЌЙцЖЈУПжмдЫЖЏ15аЁЪБвдЩЯЃЈКЌ15аЁЪБЃЉЕФГЦЮЊЁАдЫЖЏКЯИёепЁБЃЌЦфжаУПжмдЫЖЏ25аЁЪБвдЩЯЃЈКЌ25аЁЪБЃЉЕФГЦЮЊЁАдЫЖЏДяШЫЁБ.
ЙВ6зщНјааЭГМЦЃЌЕУЕНФаЩњЁЂХЎЩњУПжмдЫЖЏЕФЪБГЄЕФЭГМЦШчЯТЃЈБэ1ЁЂ2ЃЉЃЌЙцЖЈУПжмдЫЖЏ15аЁЪБвдЩЯЃЈКЌ15аЁЪБЃЉЕФГЦЮЊЁАдЫЖЏКЯИёепЁБЃЌЦфжаУПжмдЫЖЏ25аЁЪБвдЩЯЃЈКЌ25аЁЪБЃЉЕФГЦЮЊЁАдЫЖЏДяШЫЁБ.
Бэ1ЃКФаЩњ
ЪБГЄ |
|
|
|
|
|
|
ШЫЪ§ | 2 | 8 | 16 | 8 | 4 | 2 |
Бэ2ЃКХЎЩњ
ЪБГЄ |
|
|
|
|
|
|
ШЫЪ§ | 0 | 4 | 12 | 12 | 8 | 4 |
ЃЈ1ЃЉДгУПжмдЫЖЏЪБГЄВЛаЁгк20аЁЪБЕФФаЩњжаЫцЛњбЁШЁ2ШЫЃЌЧѓбЁЕНЁАдЫЖЏДяШЫЁБЕФИХТЪЃЛ
ЃЈ2ЃЉИљОнЬтФПЬѕМўЃЌЭъГЩЯТУц![]() СаСЊБэЃЌВЂХаЖЯФмЗёга99%ЕФАбЮеШЯЮЊБОаЃДѓбЇЩњЪЧЗёЮЊЁАдЫЖЏКЯИёепЁБгыадБ№гаЙи.
СаСЊБэЃЌВЂХаЖЯФмЗёга99%ЕФАбЮеШЯЮЊБОаЃДѓбЇЩњЪЧЗёЮЊЁАдЫЖЏКЯИёепЁБгыадБ№гаЙи.
УПжмдЫЖЏЕФЪБГЄаЁгк15аЁЪБ | УПжмдЫЖЏЕФЪБГЄВЛаЁгк15аЁЪБ | змМЦ | |
ФаЩњ | |||
ХЎЩњ | |||
змМЦ |
ВЮПМЙЋЪНЃК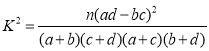 ЃЌЦфжа
ЃЌЦфжа![]() .
.
ВЮПМЪ§ОнЃК
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |