题目内容
【题目】已知曲线![]() 的参数方程为
的参数方程为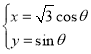 (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换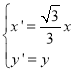 得到曲线
得到曲线![]() ,以原点为极点,
,以原点为极点,![]() 轴的正半轴为极轴,建立极坐标系.设
轴的正半轴为极轴,建立极坐标系.设![]() 点的极坐标为
点的极坐标为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(1)![]() 的极坐标方程为:
的极坐标方程为:![]() (2)
(2)![]()
【解析】
(1) 由曲线![]() 的参数方程得出其普通方程,利用坐标变换得出
的参数方程得出其普通方程,利用坐标变换得出![]() 的方程,再转化为极坐标方程;
的方程,再转化为极坐标方程;
(2)利用直线的参数方程的参数的几何意义求解即可.
解:(1)曲线![]() 的普通方程为:
的普通方程为:![]() ,
,
将曲线![]() 上的点按坐标变换
上的点按坐标变换 得到
得到 ,代入
,代入![]() 得
得![]() 的方程为:
的方程为:![]() .
.
化为极坐标方程为:![]() .
.
(2)点![]() 在直角坐标的坐标为
在直角坐标的坐标为![]() ,
,
因为直线![]() 过点
过点![]() 且倾斜角为
且倾斜角为![]() ,
,
设直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),
代入![]() 得:
得:![]() .
.
设![]() 两点对应的参数分别为
两点对应的参数分别为![]() ,
,
则![]() .
.
所以![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】2019年11月份,全国工业生产者出厂价格同比下降![]() ,环比下降
,环比下降![]() 某企业在了解市场动态之后,决定根据市场动态及时作出相应调整,并结合企业自身的情况作出相应的出厂价格,该企业统计了2019年1~10月份产品的生产数量
某企业在了解市场动态之后,决定根据市场动态及时作出相应调整,并结合企业自身的情况作出相应的出厂价格,该企业统计了2019年1~10月份产品的生产数量![]() (单位:万件)以及销售总额
(单位:万件)以及销售总额![]() (单位:十万元)之间的关系如下表:
(单位:十万元)之间的关系如下表:
| 2.08 | 2.12 | 2.19 | 2.28 | 2.36 | 2.48 | 2.59 | 2.68 | 2.80 | 2.87 |
| 4.25 | 4.37 | 4.40 | 4.55 | 4.64 | 4.75 | 4.92 | 5.03 | 5.14 | 5.26 |
(1)计算![]() 的值;
的值;
(2)计算相关系数![]() ,并通过
,并通过![]() 的大小说明
的大小说明![]() 与
与![]() 之间的相关程度;
之间的相关程度;
(3)求![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,并推测当产量为3.2万件时销售额为多少.(该问中运算结果保留两位小数)
,并推测当产量为3.2万件时销售额为多少.(该问中运算结果保留两位小数)
附:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为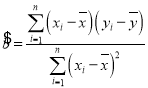 ,
,![]() ;
;
相关系数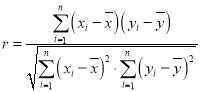 .
.
参考数据: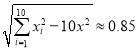 ,
,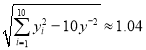 ,
,![]() .
.