题目内容
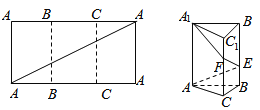
【题目】如图,把长为6,宽为3的矩形折成正三棱柱![]() ,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱
,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱![]() 的交点记为E,F.
的交点记为E,F.
(1)求三棱柱![]() 的体积;
的体积;
(2)求三棱柱中异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】
(1)根据对折的方法可求出正三棱柱![]() 的底面正三角形的边长,最后利用棱柱的体积公式求出即可.
的底面正三角形的边长,最后利用棱柱的体积公式求出即可.
(2)建立空间直角坐标系,利用空间向量的夹角公式求出即可.
(1)由操作可知;该正三棱柱的底面是边长2的正三角形,高为3.因此体积为:
![]() ;
;
(2) 因为矩形的对角线和三棱柱的侧棱![]() 的交点记为E,F.
的交点记为E,F.
所以![]()
以![]() 为坐标原点,在平面
为坐标原点,在平面![]() 内,过
内,过![]() 作
作![]() 的垂线为
的垂线为![]() 轴,以
轴,以![]() 所在直线为
所在直线为![]() 轴,以
轴,以![]() 所在直线为
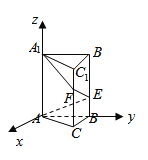
所在直线为![]() 建立如图所示的空间直角坐标系,如下图:
建立如图所示的空间直角坐标系,如下图:
![]()
![]()
设三棱柱中异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
,

![]() .
.
所以三棱柱中异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】某市对各老旧小区环境整治效果进行满意度测评,共有10000人参加这次测评(满分100分,得分全为整数).为了解本次测评分数情况,从中随机抽取了部分人的测评分数进行统计,整理见下表:
组别 | 分组 | 频数 | 频率 |
1 |
| 3 | 0.06 |
2 |
| 15 | 0.3 |
3 |
| 21 |
|
4 |
| 3 | 0.12 |
5 |
|
| 0.1 |
合计 |
| 1.00 | |
(1)求出表中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若分数在80(含80分)以上表示对该项目“非常满意”,其中分数在90(含90分)以上表示“十分满意”,现从被抽取的“非常满意“人群中随机抽取2人,求至少有一人分数是“十分满意”的概率;
(3)请你根据样本数据估计全市的平均测评分数
【题目】近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积 | 1 | 2 | 3 | 4 | 5 |
管理时间 | 8 | 10 | 13 | 25 | 24 |
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 | 150 | 50 |
女性村民 | 50 |
(1)求出相关系数![]() 的大小,并判断管理时间
的大小,并判断管理时间![]() 与土地使用面积
与土地使用面积![]() 是否线性相关?
是否线性相关?
(2)是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性?
(3)若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取3人,记取到不愿意参与管理的男性村民的人数为![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
参考公式:

![]()
其中![]() 。临界值表:
。临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考数据:![]()