题目内容
(12分)已知椭圆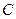 的中心在原点,焦点在
的中心在原点,焦点在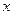 轴上,点
轴上,点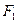 、
、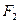 分别是椭圆的左、右焦点,在椭圆
分别是椭圆的左、右焦点,在椭圆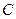 的右准线上的点
的右准线上的点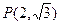 ,满足线段
,满足线段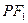 的中垂线过点
的中垂线过点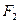 .直线
.直线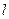 :
: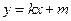 为动直线,且直线
为动直线,且直线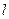 与椭圆
与椭圆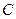 交于不同的两点
交于不同的两点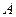 、
、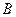 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆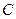 上存在点
上存在点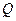 ,满足
,满足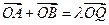 (
(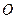 为坐标原点),
为坐标原点),
求实数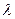 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,当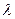 取何值时,
取何值时,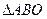 的面积最大,并求出这个最大值.
的面积最大,并求出这个最大值.
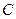 的中心在原点,焦点在
的中心在原点,焦点在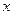 轴上,点
轴上,点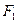 、
、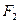 分别是椭圆的左、右焦点,在椭圆
分别是椭圆的左、右焦点,在椭圆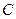 的右准线上的点
的右准线上的点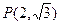 ,满足线段
,满足线段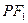 的中垂线过点
的中垂线过点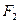 .直线
.直线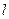 :
: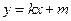 为动直线,且直线
为动直线,且直线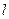 与椭圆
与椭圆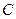 交于不同的两点
交于不同的两点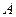 、
、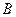 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆
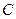 上存在点
上存在点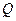 ,满足
,满足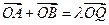 (
(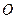 为坐标原点),
为坐标原点),求实数
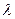 的取值范围;
的取值范围;(Ⅲ)在(Ⅱ)的条件下,当
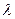 取何值时,
取何值时,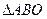 的面积最大,并求出这个最大值.
的面积最大,并求出这个最大值.(Ⅰ)所求椭圆方程为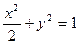 。
。
(Ⅱ)实数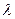 的取值范围是
的取值范围是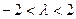 .
.
(Ⅲ)当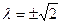 时,
时,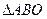 的面积最大,最大值为
的面积最大,最大值为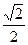 .
.
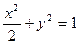 。
。(Ⅱ)实数
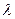 的取值范围是
的取值范围是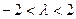 .
.(Ⅲ)当
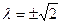 时,
时,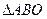 的面积最大,最大值为
的面积最大,最大值为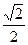 .
.解:(Ⅰ)设椭圆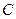 的方程为
的方程为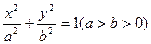 ,半焦距为
,半焦距为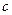 ,依题意有
,依题意有
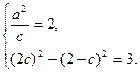 解得
解得
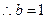 .
.
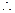 所求椭圆方程为
所求椭圆方程为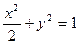 . ……………………………3分
. ……………………………3分
(Ⅱ)由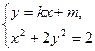 ,得
,得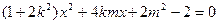 .
.
设点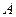 、
、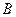 的坐标分别为
的坐标分别为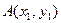 、
、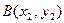 ,则
,则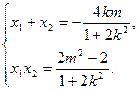 ……4分
……4分
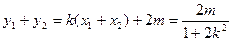 .
.
(1)当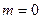 时,点
时,点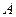 、
、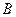 关于原点对称,则
关于原点对称,则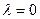 .
.
(2)当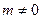 时
时 ,点
,点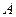 、
、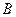 不关于原点对称,则
不关于原点对称,则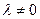 ,
,
由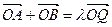 ,得
,得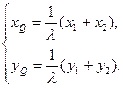 即
即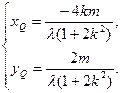
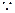 点
点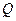 在椭圆上,
在椭圆上,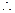 有
有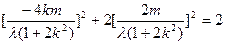 ,
,
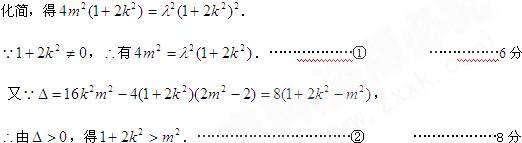 将①、②两式,得
将①、②两式,得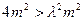 .
.
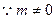 ,
,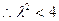 ,则
,则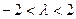 且
且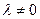 .
.
综合(1)、(2)两种情况,得实数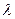 的取值范围是
的取值范围是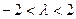 . ………………9分
. ………………9分
【注】 此题可根据图形得出当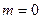 时
时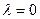 ,当
,当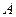 、
、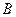 两点重合时
两点重合时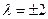 .
.
如果学生由此得出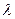 的取值范围是
的取值范围是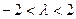 可酌情给分.
可酌情给分.
(Ⅲ)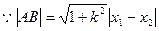 ,点
,点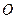 到直线
到直线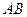 的距离
的距离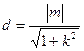 ,
,
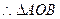 的面积
的面积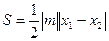
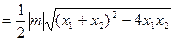
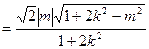 . ………………………… 10分
. ………………………… 10分
由①有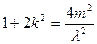 ,代入上式并化简,得
,代入上式并化简,得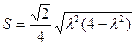 .
.
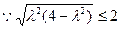 ,
,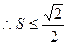 . ……………………… 11分
. ……………………… 11分
当且仅当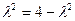 ,即
,即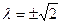 时,等号成立.
时,等号成立.
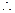 当
当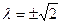 时,
时,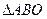 的面积最大,最大值为
的面积最大,最大值为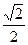 . ……………………… 12分
. ……………………… 12分
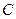 的方程为
的方程为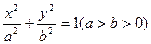 ,半焦距为
,半焦距为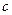 ,依题意有
,依题意有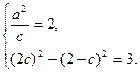 解得
解得
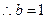 .
.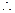 所求椭圆方程为
所求椭圆方程为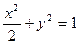 . ……………………………3分
. ……………………………3分(Ⅱ)由
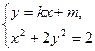 ,得
,得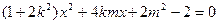 .
.设点
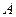 、
、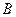 的坐标分别为
的坐标分别为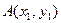 、
、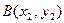 ,则
,则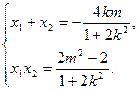 ……4分
……4分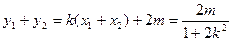 .
.(1)当
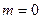 时,点
时,点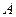 、
、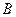 关于原点对称,则
关于原点对称,则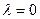 .
.(2)当
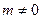 时
时 ,点
,点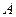 、
、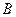 不关于原点对称,则
不关于原点对称,则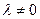 ,
,由
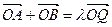 ,得
,得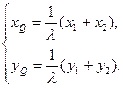 即
即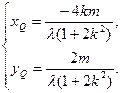
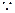 点
点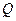 在椭圆上,
在椭圆上,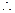 有
有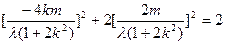 ,
,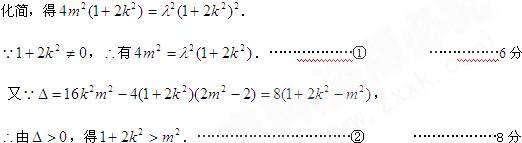 将①、②两式,得
将①、②两式,得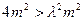 .
.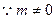 ,
,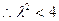 ,则
,则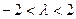 且
且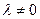 .
.综合(1)、(2)两种情况,得实数
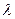 的取值范围是
的取值范围是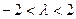 . ………………9分
. ………………9分【注】 此题可根据图形得出当
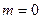 时
时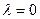 ,当
,当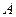 、
、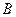 两点重合时
两点重合时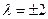 .
.如果学生由此得出
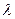 的取值范围是
的取值范围是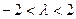 可酌情给分.
可酌情给分.(Ⅲ)
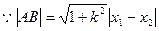 ,点
,点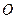 到直线
到直线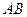 的距离
的距离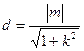 ,
,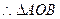 的面积
的面积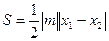
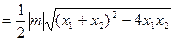
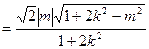 . ………………………… 10分
. ………………………… 10分由①有
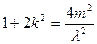 ,代入上式并化简,得
,代入上式并化简,得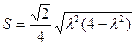 .
.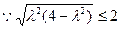 ,
,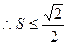 . ……………………… 11分
. ……………………… 11分当且仅当
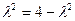 ,即
,即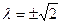 时,等号成立.
时,等号成立. 当
当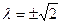 时,
时,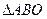 的面积最大,最大值为
的面积最大,最大值为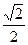 . ……………………… 12分
. ……………………… 12分
练习册系列答案
相关题目
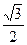 ,与直线x+y-1=0相交于两点M、N,且OM⊥ON.求椭圆的方程。
,与直线x+y-1=0相交于两点M、N,且OM⊥ON.求椭圆的方程。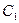 :
: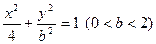 的离心率等于
的离心率等于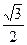 ,抛物线
,抛物线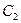 :
: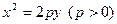 的焦点在椭圆的顶点上。
的焦点在椭圆的顶点上。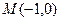 的直线
的直线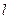 与抛物线
与抛物线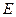 、
、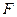 两点,又过
两点,又过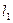 、
、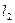 ,当
,当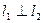 时,求直线
时,求直线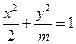 的离心率为
的离心率为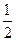 ,则m=" " ( )
,则m=" " ( )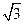 B
B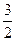 C
C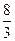 D
D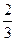
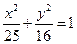 的左右焦点分别为
的左右焦点分别为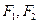 ,弦
,弦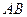 过
过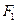 ,若
,若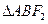 的内切圆周长为
的内切圆周长为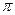 ,
,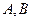 两点的坐标分别为
两点的坐标分别为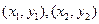 ,则
,则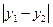 值为()
值为()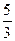
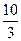
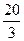
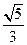
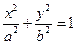 的左焦点
的左焦点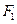 ,右顶点A,上顶点B,且
,右顶点A,上顶点B,且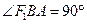 ,则椭圆的离心率是
,则椭圆的离心率是



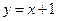 被椭圆
被椭圆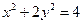 所截得的弦的中点坐标是 ( )
所截得的弦的中点坐标是 ( )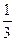 ,
,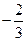 )
)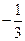 ,
,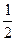 )
)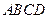 ,则以
,则以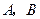 为焦点,且过
为焦点,且过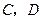 两点的椭圆的离心率为______.
两点的椭圆的离心率为______.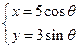 (
(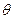 为参数),则它的离心率为 .
为参数),则它的离心率为 .