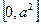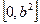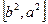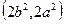题目内容
中心在坐标原点,焦点在x轴上的椭圆,它的离心率为 ,与直线x+y-1=0相交于两点M、N,且OM⊥ON.求椭圆的方程。
,与直线x+y-1=0相交于两点M、N,且OM⊥ON.求椭圆的方程。
 ,与直线x+y-1=0相交于两点M、N,且OM⊥ON.求椭圆的方程。
,与直线x+y-1=0相交于两点M、N,且OM⊥ON.求椭圆的方程。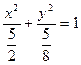
设中心在坐标原点,焦点在x轴上的椭圆方程为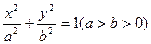 .
.
∵离心率e= ∴a=2b
∴a=2b
∴椭圆的方程可化为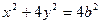
设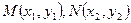 ,由于点M、N都在直线x+y-1=0上,
,由于点M、N都在直线x+y-1=0上,
因此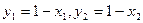 ,
,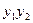 =
=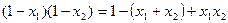
∵OM⊥ON,
∴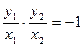 即
即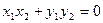
即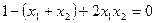
将直线x+y-1=0与椭圆的方程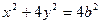 联立消取y,得
联立消取y,得
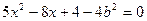
∵M、N是直线与椭圆的两交点
∴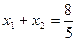 ,
,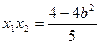 代入
代入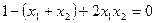 得
得
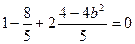 解得
解得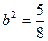 ,∴
,∴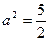
∴所要求的椭圆方程为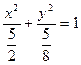 .
.
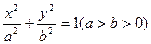 .
.∵离心率e=
 ∴a=2b
∴a=2b∴椭圆的方程可化为
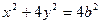
设
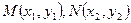 ,由于点M、N都在直线x+y-1=0上,
,由于点M、N都在直线x+y-1=0上,因此
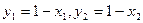 ,
,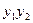 =
=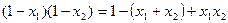
∵OM⊥ON,
∴
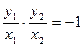 即
即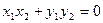
即
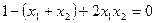
将直线x+y-1=0与椭圆的方程
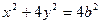 联立消取y,得
联立消取y,得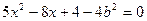
∵M、N是直线与椭圆的两交点
∴
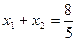 ,
,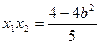 代入
代入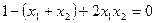 得
得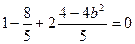 解得
解得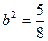 ,∴
,∴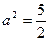
∴所要求的椭圆方程为
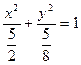 .
.
练习册系列答案
相关题目
 的右准线是
的右准线是 ,倾斜角为
,倾斜角为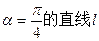 交椭圆于A、B两点,AB的中点为
交椭圆于A、B两点,AB的中点为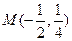
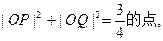 若直线OP、OQ的斜率分别为
若直线OP、OQ的斜率分别为 ,求证:
,求证: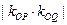 是定值。
是定值。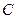 的中心在原点,焦点在
的中心在原点,焦点在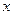 轴上,点
轴上,点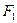 、
、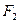 分别是椭圆的左、右焦点,在椭圆
分别是椭圆的左、右焦点,在椭圆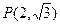 ,满足线段
,满足线段 的中垂线过点
的中垂线过点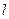 :
: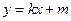 为动直线,且直线
为动直线,且直线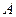 、
、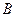 .
.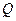 ,满足
,满足 (
( 为坐标原点),
为坐标原点),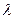 的取值范围;
的取值范围;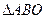 的面积最大,并求出这个最大值.
的面积最大,并求出这个最大值.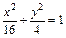 上的点到直线
上的点到直线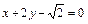 的最大距离是 ( )
的最大距离是 ( )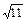
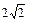
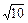
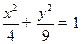 的上.下两个焦点分别为
的上.下两个焦点分别为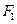 .
.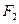 ,点
,点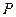 为该椭圆上一点,若
为该椭圆上一点,若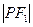 .
.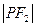 为方程
为方程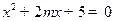 的两根,则
的两根,则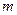 = .
= .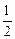
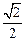
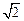
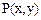 是椭圆
是椭圆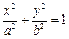 (
( 上的任意一点,
上的任意一点, 是椭圆的两个焦点,且∠
是椭圆的两个焦点,且∠ ,则该椭圆的离心率的取值范围是
,则该椭圆的离心率的取值范围是 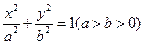 上任意一点,
上任意一点,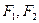 是其两个焦点,则
是其两个焦点,则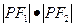 的取值范围是( )
的取值范围是( )