题目内容
已知正项数列{an}满足a1=1,(n+2)an+12-(n+1)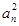 +anan+1=0,则它的通项公式为( ).
+anan+1=0,则它的通项公式为( ).
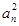 +anan+1=0,则它的通项公式为( ).
+anan+1=0,则它的通项公式为( ).A.an=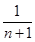 | B.an=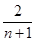 |
C.an=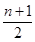 | D.an=n |
B
由(n+2) -(n+1)
-(n+1)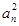 +anan+1=0,得(n+2)·
+anan+1=0,得(n+2)· +
+ =n+1,即
=n+1,即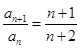 ,则an=
,则an= .
.
 -(n+1)
-(n+1)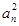 +anan+1=0,得(n+2)·
+anan+1=0,得(n+2)· +
+ =n+1,即
=n+1,即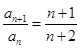 ,则an=
,则an= .
.
练习册系列答案
相关题目
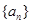 的前
的前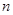 项和为
项和为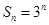 ,数列
,数列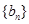 满足:
满足: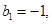
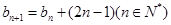 。
。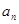 ;
;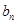 ;(3)若
;(3)若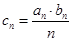 ,求数列
,求数列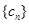 的前
的前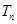 .
.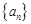 的前
的前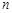 项和
项和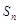 满足
满足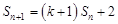 ,又
,又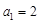 ,
,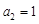 .
.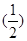 n-1=2(n∈N*),设cn=2nan.
n-1=2(n∈N*),设cn=2nan.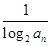 ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得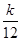 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.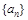 中,
中,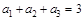 ,
,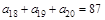 ,则该数列前20项的和为____.
,则该数列前20项的和为____.