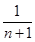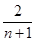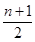题目内容
已知Sn是数列{an}的前n项和,且an=Sn-1+2(n≥2),a1=2.
(1)求数列{an}的通项公式.
(2)设bn=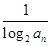 ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
对于任意的正整数n,有Tn>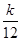 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.
(1)求数列{an}的通项公式.
(2)设bn=
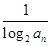 ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>
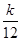 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.(1)2n(2)存在
(1)由已知an=Sn-1+2, ①
得an+1=Sn+2. ②
②-①,得an+1-an=Sn-Sn-1(n≥2),
∴an+1=2an(n≥2).
又a1=2,∴a2=a1+2=4=2a1,
∴an+1=2an(n=1,2,3,…),
∴数列{an}是一个以2为首项,2为公比的等比数列,
∴an=2·2n-1=2n,n∈N*.
(2)bn=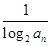 =
=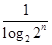 =
=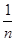 ,∴Tn=bn+1+bn+2+…+b2n=
,∴Tn=bn+1+bn+2+…+b2n=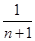 +
+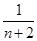 +…+
+…+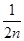 ,Tn+1=bn+2+bn+3+…+b2(n+1)=
,Tn+1=bn+2+bn+3+…+b2(n+1)=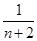 +
+ +…+
+…+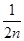 +
+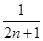 +
+ .
.
∴Tn+1-Tn=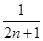 +
+ -
-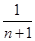 =
= =
= .
.
∵n是正整数,∴Tn+1-Tn>0,即Tn+1>Tn.
∴数列{Tn}是一个单调递增数列.又T1=b2=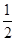 ,∴Tn≥T1=
,∴Tn≥T1=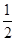 ,
,
要使Tn>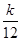 恒成立,则
恒成立,则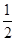 >
>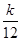 ,即k<6.又k是正整数,故存在最大正整数k=5使Tn>
,即k<6.又k是正整数,故存在最大正整数k=5使Tn>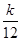 恒成立.
恒成立.
得an+1=Sn+2. ②
②-①,得an+1-an=Sn-Sn-1(n≥2),
∴an+1=2an(n≥2).
又a1=2,∴a2=a1+2=4=2a1,
∴an+1=2an(n=1,2,3,…),
∴数列{an}是一个以2为首项,2为公比的等比数列,
∴an=2·2n-1=2n,n∈N*.
(2)bn=
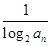 =
=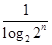 =
=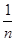 ,∴Tn=bn+1+bn+2+…+b2n=
,∴Tn=bn+1+bn+2+…+b2n=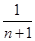 +
+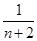 +…+
+…+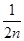 ,Tn+1=bn+2+bn+3+…+b2(n+1)=
,Tn+1=bn+2+bn+3+…+b2(n+1)=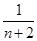 +
+ +…+
+…+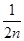 +
+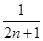 +
+ .
.∴Tn+1-Tn=
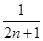 +
+ -
-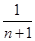 =
= =
= .
.∵n是正整数,∴Tn+1-Tn>0,即Tn+1>Tn.
∴数列{Tn}是一个单调递增数列.又T1=b2=
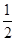 ,∴Tn≥T1=
,∴Tn≥T1=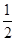 ,
,要使Tn>
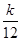 恒成立,则
恒成立,则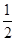 >
>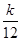 ,即k<6.又k是正整数,故存在最大正整数k=5使Tn>
,即k<6.又k是正整数,故存在最大正整数k=5使Tn>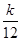 恒成立.
恒成立.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
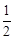 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.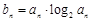 ,数列{bn}的前n项和Tn,求满足不等式
,数列{bn}的前n项和Tn,求满足不等式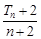 ≥
≥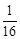 的最大n值.
的最大n值.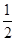 a11+6,则数列{an}前9项的和S9等于( ).
a11+6,则数列{an}前9项的和S9等于( ).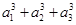 +…+
+…+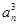 =
=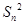 ,记Sn为数列{an}的前n项和.
,记Sn为数列{an}的前n项和.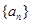 的前
的前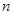 项和为
项和为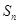 ,且
,且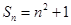 ,则
,则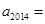 .
.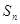 为等差数列
为等差数列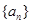 的前
的前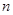 项和,
项和,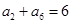 ,则
,则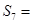 .
.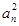 +anan+1=0,则它的通项公式为( ).
+anan+1=0,则它的通项公式为( ).