题目内容
设数列{an}是公差不为零的等差数列,Sn是数列{an}的前n项和,且S=9S2,S4=4S2,则数列{an}的通项公式为________.
an=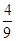 (2n-1)
(2n-1)
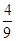 (2n-1)
(2n-1)设等差数列{an}的公差为d,由Sn=na1+ d及已知条件得(3a1+3d)2=9(2a1+d).①
d及已知条件得(3a1+3d)2=9(2a1+d).①
4a1+6d=4(2a1+d).②
由②得d=2a1,代入①有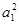 =
=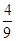 a1,解得a1=0或a1=
a1,解得a1=0或a1=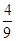 .
.
当a1=0时,d=0,舍去.因此a1=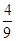 ,d=
,d= .
.
故数列{an}的通项公式为an=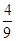 +(n-1)·
+(n-1)· =
=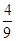 (2n-1).
(2n-1).
 d及已知条件得(3a1+3d)2=9(2a1+d).①
d及已知条件得(3a1+3d)2=9(2a1+d).①4a1+6d=4(2a1+d).②
由②得d=2a1,代入①有
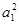 =
=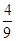 a1,解得a1=0或a1=
a1,解得a1=0或a1=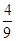 .
.当a1=0时,d=0,舍去.因此a1=
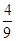 ,d=
,d= .
.故数列{an}的通项公式为an=
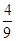 +(n-1)·
+(n-1)· =
=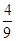 (2n-1).
(2n-1).
练习册系列答案
相关题目
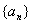 的首项
的首项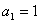 ,前
,前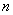 项和为
项和为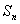 (
(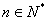 ),且点
),且点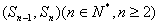 在直线
在直线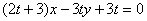 上(
上(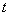 为与
为与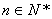 )为等比数列;
)为等比数列;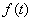 ,数列
,数列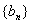 满足
满足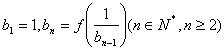 ,设
,设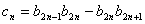 ,求数列
,求数列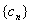 的前
的前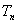 ;
;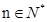 时不等式
时不等式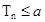 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。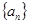 的各项均为正数,且
的各项均为正数,且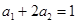 ,
,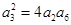 .
.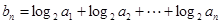 ,求数列
,求数列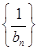 的前
的前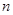 项和.
项和.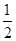
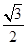
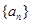 的前
的前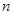 项和为
项和为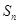 ,且
,且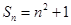 ,则
,则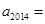 .
.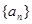 中,
中,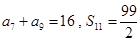 , 则
, 则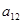 的值是( )
的值是( )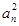 +anan+1=0,则它的通项公式为( ).
+anan+1=0,则它的通项公式为( ).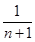
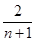
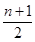
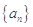 中,
中,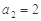 ,
,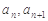 是方程
是方程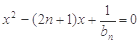 的两个根,则数列
的两个根,则数列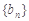 的前
的前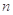 项和
项和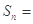 _________.
_________.