题目内容
6.全集U=R,若集合A={x|3<x≤10},B={x|2<x≤7}.(1)求A∩B,A∪B;
(2)求(∁UA)∪B,(∁UA)∪(∁UB)
(3)若集合C={x|x>a},B⊆C,求实数a的取值范围.
分析 (1)直接由交、并集运算得答案;
(2)先求出∁UA,∁UB,再由并集运算得答案;
(3)直接利用两集合端点值间的关系得答案.
解答 解:全集U=R,集合A={x|3<x≤10},B={x|2<x≤7}.
(1)A∩B={x|3<x≤7},A∪B={x|2<x≤10};
(2)∁UA={x|x≤3或x>10},∁UB={x|x≤2或x>7},
∴(∁UA)∪B={x|x≤7或x>10},(∁UA)∪(∁UB)={x|x≤3或x>7};
(3)集合C={x|x>a},且B⊆C,则a≤2.
点评 本题考查交、并、补集的混合运算,是基础的计算题.

练习册系列答案
相关题目
1.计算lg$\frac{5}{2}$+2lg2-($\frac{1}{2}$)-1=( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
18.已知映射f:x→lgx+1,则像2在f作用下的原像为( )
| A. | lg2+1 | B. | 1 | C. | 10 | D. | 100 |
16.函数f(x)=lo${g}_{\frac{1}{2}}$(x2-ax)在区间[2,4]上是减函数,则实数a的取值范围是( )
| A. | 2<a≤4 | B. | a≤4 | C. | a<2 | D. | a≤2 |
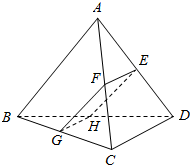 如图,三棱锥A-BCD中,对棱AB与CD所成角为60°,且AB=CD=α,该三棱锥被一平面所截,截面为平行四边形EFGH.
如图,三棱锥A-BCD中,对棱AB与CD所成角为60°,且AB=CD=α,该三棱锥被一平面所截,截面为平行四边形EFGH.