题目内容
1.函数f(x)=3x+5x的零点所在的区间是(-1,0).分析 根据函数f(x)=3x+5x是R上的连续函数,且单调递增,f(-1)f(0)<0,结合函数零点的判定定理,可得结论.
解答 解:∵函数f(x)=3x+5x是R上的连续函数,且单调递增,
f(-1)=3-1+5×(-1)=-$\frac{16}{3}$<0,f(0)=30+0=1>0,
∴f(-1)f(0)<0.
∴f(x)=3x+5x的零点所在的一个区间为(-1,0),
故答案为:(-1,0).
点评 本题考查了函数零点的概念与零点定理的应用,属于容易题.

练习册系列答案
相关题目
9.过椭圆$\frac{{x}^{2}}{4}+{y}^{2}=1$焦点且与椭圆长轴垂直的直线与椭圆相交于A、B两点,则|AB|等于( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 1 | D. | 4$\sqrt{3}$ |
16.椭圆上长轴两端点视角为120°的点的个数可能为( )
| A. | 2 | B. | 4 | C. | 0、2或4 | D. | 2或4 |
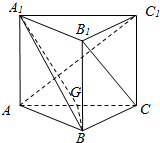 如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.
如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.