题目内容
9.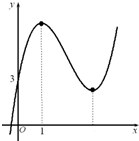 已知函数f(x)=ax3+bx2+(c-3a-2b)x+d的图象如图所示.
已知函数f(x)=ax3+bx2+(c-3a-2b)x+d的图象如图所示.(1)求c,d的值;
(2)若函数f(x)在x=2处的切线方程为3x+y-11=0,求函数f(x)的解析式;
(3)在(2)的条件下,函数y=f(x)与y=$\frac{1}{3}$f′(x)+5x+m的图象有三个不同的交点,求m的取值范围.
分析 (1)求导函数,利用函数f(x)的图象过点(0,3),且f′(1)=0,建立方程,即可求c,d的值;
(2)利用函数f(x)在x=2处的切线方程为3x+y-11=0,建立方程,即可求出a,b,从而可求函数f(x)的解析式.
(3)求导后得到函数的极值点,求出极大值和极小值利用数形结合的解题思想得到答案.
解答 解:函数f(x)的导函数为f′(x)=3ax2+2bx+c-3a-2b…(3分)
(1)由图可知,函数f(x)的图象过点(0,3),且f′(1)=0
∴$\left\{\begin{array}{l}{d=3}\\{3a+2b+c-3a-2b=0}\end{array}\right.$,可得$\left\{\begin{array}{l}{d=3}\\{c=0}\end{array}\right.$.…(7分)
(2)依题意 f′(2)=-3且f(2)=5,
∴$\left\{\begin{array}{l}{12a+4b-3a-2b=-3}\\{8a+4b-6a-4b+3=5}\end{array}\right.$
解得a=1,b=-6,
∴f(x)=x3-6x2+9x+3…(12分)
(3)f′(x)=3x2-12x+9.可转化为:x3-6x2+9x+3=(x2-4x+3)+5x+m有三个不等实根,即:g(x)=x3-7x2+8x-m与x轴有三个交点;
g′(x)=3x2-14x+8=(3x-2)(x-4),
| x | (-∞,$\frac{2}{3}$) | $\frac{2}{3}$ | ($\frac{2}{3}$,4) | 4 | (4,+∞) |
| g′(x) | + | 0 | - | 0 | + |
| g(x) | 增 | 极大值 | 减 | 极小值 | 增 |
当且仅当g($\frac{2}{3}$)=$\frac{68}{27}-m$>0,且g(4)=-16-m<0时,有三个交点,故而,-16<m<$\frac{68}{27}$.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查函数的解析式,属于中档题.

练习册系列答案
相关题目
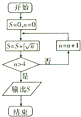
14.阅读如图所示的算法框图,运行相应的程序,则循环体执行的次数是( )
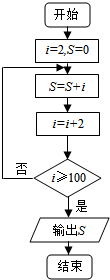

| A. | 50 | B. | 49 | C. | 100 | D. | 98 |
1.函数$y=sin(-3x+\frac{π}{4})$的最小正周期是( )
| A. | $\frac{2π}{3}$ | B. | $-\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $-\frac{π}{3}$ |
18.${∫}_{0}^{1}$(ex+2x)dx等于( )
| A. | 1 | B. | e-1 | C. | e | D. | e+1 |