题目内容
8.实数x,y满足$\left\{\begin{array}{l}{x≥1}\\{y≤a(a>1)}\\{x-y≤0}\end{array}\right.$,若目标函数z=x+y取得最大值4,则实数a的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 作出不等式组表示的可行域,将目标函数变形y=-x+z,判断出z表示直线的纵截距,结合图象,求出k的范围.
解答 解:作出不等式组表示的平面区域,如图所示:
∵y=-x+z,则z表示直线的纵截距
做直线L:x+y=0,然后把直线L向可行域平移,结合图象可知,平移到C(a,a)时,z最大
此时z=2a=4
∴a=2
故选:B.
点评 解决此类问题的关键是正确画出不等式组表示的可行域,将目标函数赋予几何意义.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
16.已知命题p:若a=$\frac{π}{6}$,则sina=$\frac{1}{2}$;命题q:若sina=$\frac{1}{2}$,则a=$\frac{π}{6}$.下面四个结论中正确的是( )
| A. | p∧q是真命题 | B. | p∨q是真命题 | C. | ¬p是真命题 | D. | ¬q是假命题 |
13.已知集合A={x|x2-3x+2<0},B={x|log4x>$\frac{1}{2}$},则( )
| A. | A⊆B | B. | B⊆A | C. | A∩∁RB=R | D. | A∩B=∅ |
20.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左右焦点分别为F1(-c,0),F2(c,0),若双曲线右支上存在异于顶点的点P满足c•sin∠PF1F2=3a•sin∠PF2F1,则双曲线的离心率的取值范围是( )
| A. | $(1,1+\sqrt{7})$ | B. | $(1,2+\sqrt{7})$ | C. | $(3,1+\sqrt{7})$ | D. | (3,2+$\sqrt{7}$) |
15. 电流强度I(安)随时间t(秒)变化的函数$I=Asin({ωt+\frac{π}{6}})$(A>0,ω≠0)的图象如图,则当$t=\frac{1}{50}$时电流强度是( )
电流强度I(安)随时间t(秒)变化的函数$I=Asin({ωt+\frac{π}{6}})$(A>0,ω≠0)的图象如图,则当$t=\frac{1}{50}$时电流强度是( )
 电流强度I(安)随时间t(秒)变化的函数$I=Asin({ωt+\frac{π}{6}})$(A>0,ω≠0)的图象如图,则当$t=\frac{1}{50}$时电流强度是( )
电流强度I(安)随时间t(秒)变化的函数$I=Asin({ωt+\frac{π}{6}})$(A>0,ω≠0)的图象如图,则当$t=\frac{1}{50}$时电流强度是( )| A. | 5安 | B. | -5安 | C. | $5\sqrt{3}$安 | D. | 10安 |
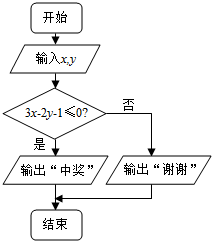 某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、200人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取10人在前排就坐,其中高二代表队有5人.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、200人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取10人在前排就坐,其中高二代表队有5人.