题目内容
【题目】（本小题满分12分）假设关于某设备使用年限x（年）和所支出的维修费用y（万元）有如下统计资料：
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知，y对x呈线性相关关系，试求：
（1）回归直线方程；
（2）估计使用年限为10年时，维修费用约是多少？
【答案】（1）
（2）1238万元
【解析】
(1)根据题表中数据作散点图，如图所示：
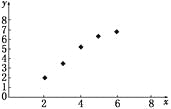
从散点图可以看出，样本点都集中分布在一条直线附近，因此y与x之间具有线性相关关系．利用题中数据得：
(2＋3＋4＋5＋6)＝4，
＝(2.2＋3.8＋5.5＋6.5＋7.0)＝5，
2×2.2＋3×3.8＋4×5.5＋5×6.5＋6×7.0＝112.3，
＝22＋32＋42＋52＋62＝90，
所以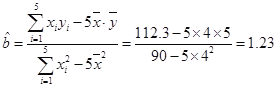
，
，
∴线性回归方程为
.
(2)当x＝10时，
＝1.23×10＋0.08＝12.38(万元)，即当使用10年时，估计维修费用是12.38万元．
练习册系列答案
教材全解字词句篇系列答案
相关题目
【题目】探究函数
，x∈(0，+∞)取最小值时x的值，列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点，完成以下的问题:
(1)函数(x>0)在区间(0，2)上递减；函数
在区间________上递增.当x=_________时，
_______.
(2)证明:函数(x>0)在区间(O，2)上递减.
