题目内容
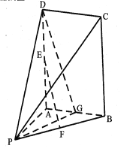
【题目】如图，在平面直角坐标系xOy中，B1，B2是椭圆
的短轴端点，P是椭圆上异于点B1，B2的一动点．当直线PB1的方程为
时，线段PB1的长为
．
（1）求椭圆的标准方程；
（2）设点Q满足：QB1⊥PB1，QB2⊥PB2，求证：△PB1B2与△QB1B2的面积之比为定值．
【答案】（1）
；（2）2
【解析】试题分析： 
由
中，令
，得
，求出b＝3，然后
，算出
QB1的斜率为
，表示直线QB1的方程和QB2的方程，求出两点坐标关系，代入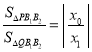
，求出结果
解析：设
， 
．
（1）在
中，令
，得
，从而b＝3．
由
得
，所以
．
因为
， 所以
，解得
．
所以椭圆的标准方程为
．
（2）直线PB1的斜率为
，由
所以直线QB1的斜率为
． 于是直线QB1的方程为： 
．
同理，QB2的方程为： 
．
联立两直线方程，消去y，得
．
因为
在椭圆
上，所以
，从而
．
所以
，所以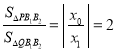
．
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
（单位：千元）对年销售量
（单位：
）和年利润
（单位：千元）的影响，对近13年的宣传费
和年销售量
数据作了初步处理，得到下面的散点图及一些统计量的值．
由散点图知，按
建立关于的回归方程是合理的．令
，则
，经计算得如下数据：
|
|
|
|
|
|
10.15 | 109.94 | 0.16 | -2.10 | 0.21 | 21.22 |
（1）根据以上信息，建立关于
的回归方程；
（2）已知这种产品的年利润与
的关系为
．根据（1）的结果，求当年宣传费
时，年利润的预报值是多少？
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为
，
．
【题目】根据教育部最新消息，2020年高考数学将是最后一年实行文理分科，由于课程大纲与命题方向出现了变动，试题难度也可能会做出相应调整.为了评估学生在2020年高考复习情况，某中学组织本校540名考生参加市模拟考试，现采用分层抽样的方法从文、理科考生中分别抽取60和30份数学试卷进行成绩分析，得到下面的成绩频数分布表：
分数分组 |
|
|
|
|
|
文科频数 | 12 | 4 | 10 | 11 | 23 |
理科频数 | 3 | 7 | 2 | 10 | 8 |
由此可估计文科考生的不及格人数（90分为及格分数线）大约为（ ）
A.128B.156C.204D.132
