题目内容
8.己知函数f(x)=xlnx.(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)对?x≥1,f(x)≤m(x2-1)成立,求实数m的最小值;
(3)证明:1n$\root{4}{2n+1}$$<\sum_{i=1}^{n}$$\frac{i}{4{i}^{2}-1}$.(n∈N*)
分析 (1)由f(1)=0,f′(1)=1;从而写出切线方程即可;
(2)化简可得m(x-$\frac{1}{x}$)-lnx≥0,从而令g(x)=m(x-$\frac{1}{x}$)-lnx,x≥1;则问题等价于?x≥1,g(x)≥0恒成立;从而求导确定函数的单调性及取值情况,从而解得.
(3)由(2)知,当m=$\frac{1}{2}$时,对?x≥1,xlnx≤$\frac{1}{2}$(x2-1)恒成立,从而化简可得lnx≤$\frac{1}{2}$$\frac{(x+1)(x-1)}{x}$(当且仅当x=1时等号成立);再设i∈N*,则$\frac{2i+1}{2i-1}$>1,从而证明.
解答 解:(1)f(1)=ln1=0,f′(1)=ln1+1=1;
故曲线f(x)在点(1,f(1))处的切线方程为y-0=x-1,
即x-y-1=0;
(2)∵x≥1,f(x)≤m(x2-1),
∴xlnx≤m(x2-1),
∴m(x-$\frac{1}{x}$)-lnx≥0,
设g(x)=m(x-$\frac{1}{x}$)-lnx,x≥1;
则问题等价于?x≥1,g(x)≥0恒成立;
注意到g(1)=0,
∵g′(x)=m(1+$\frac{1}{{x}^{2}}$)-$\frac{1}{x}$,
∵x≥1,∴$\left\{\begin{array}{l}{1+\frac{1}{{x}^{2}}>0}\\{\frac{1}{x}>0}\end{array}\right.$,
∴当m≤0时,g(x)在[1,+∞)上单调递减,
∴g(x)≤g(1)=0,故不成立;
当m>0时,g′(x)=$\frac{m{x}^{2}-x+m}{{x}^{2}}$,
令h(x)=mx2-x+m,
∵△=1-4m2,
①若△=1-4m2≤0,即m≥$\frac{1}{2}$时;
此时,h(x)≥0,故g′(x)≥0,
故g(x)在[1,+∞)上单调递增,
故g(x)≥g(1)=0,故成立;
②若△=1-4m2>0,即0<m<$\frac{1}{2}$时;
此时,h(x)=0存在两个不同的实数根x1,x2,
不妨设x1<x2,
故x1x2=1,故x1<1<x2,
故g(x)在[1,x2)上单调递减,
故g(x)≤g(1)=0,故不成立;
综上所述,实数m的最小值为$\frac{1}{2}$;
(3)证明:由(2)知,当m=$\frac{1}{2}$时,对?x≥1,xlnx≤$\frac{1}{2}$(x2-1)恒成立,
即lnx≤$\frac{1}{2}$$\frac{(x+1)(x-1)}{x}$(当且仅当x=1时等号成立);
设i∈N*,则$\frac{2i+1}{2i-1}$>1,
故ln$\frac{2i+1}{2i-1}$<$\frac{1}{2}$($\frac{2i+1}{2i-1}$+1)($\frac{2i+1}{2i-1}$-1)$\frac{2i-1}{2i+1}$=$\frac{4i}{4{i}^{2}-1}$,
故$\frac{1}{4}$ln$\frac{2i+1}{2i-1}$<$\frac{i}{4{i}^{2}-1}$,
故$\frac{1}{4}$$\sum_{i=1}^{n}(ln\frac{2i+1}{2i-1})$$<\sum_{i=1}^{n}$$\frac{i}{4{i}^{2}-1}$,
即1n$\root{4}{2n+1}$$<\sum_{i=1}^{n}$$\frac{i}{4{i}^{2}-1}$.(n∈N*).
点评 本题考查了导数的综合应用及恒成立问题,同时考查了分类讨论的思想应用及联加的应用,属于难题.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案| A. | $[\frac{1}{4},\frac{1}{3})$ | B. | $(0,\frac{1}{2})$ | C. | $(0,\frac{1}{4}]$ | D. | $(\frac{1}{3},\frac{1}{2})$ |
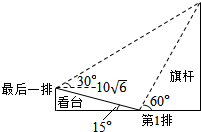 某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10m(如图所示),则旗杆的高度为( )
某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10m(如图所示),则旗杆的高度为( )| A. | 10 m | B. | 30 m | C. | 10m | D. | 10m |
| A. | $y=2{x^{\frac{1}{2}}}$ | B. | y=x3+x | C. | y=2x | D. | $y={x^{\frac{1}{2}}}$ |
 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,E是CC1的中点,F是CE的中点,F是CE的中点.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,E是CC1的中点,F是CE的中点,F是CE的中点.