题目内容
18.已知f(n)=1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}$(n∈N*),经计算得f(4)>2,f(8)>$\frac{5}{2}$,f(16)>3,f(32)>$\frac{7}{2}$,则可以归纳出一般结论:当n≥2时,有$f({2^n})>\frac{n+2}{2}$(n∈N*).分析 由题意f(4)>2,可化为f(22)>$\frac{2+2}{2}$,f(8)>$\frac{5}{2}$,可化为f(23)>$\frac{3+2}{2}$,即可得出结论.
解答 解:由题意f(4)>2,可化为f(22)>$\frac{2+2}{2}$,
f(8)>$\frac{5}{2}$,可化为f(23)>$\frac{3+2}{2}$,
…
以此类推,可得$f({2^n})>\frac{n+2}{2}$(n∈N*).
故答案为:$f({2^n})>\frac{n+2}{2}$(n∈N*).
点评 本题考查归纳推理,把已知的式子变形找规律是解决问题的关键,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.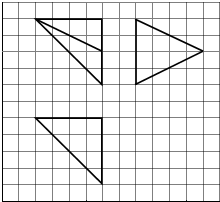 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )| A. | 8 | B. | $4\sqrt{5}$ | C. | 12 | D. | 16 |
13.已知a=log3650.99、b=1.01365、c=0.99365,则a、b、c的大小关系为( )
| A. | a<c<b | B. | b<a<c | C. | a<b<c | D. | b<c<a |
3.在等比数列{an}中,a1=3,a6=6,则a16等于( )
| A. | 6 | B. | 12 | C. | 24 | D. | 48 |
10.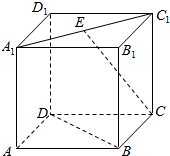 如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
 如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
8.若一个底面是正三角形的三棱柱的正视图如图所示,则体积等于( )
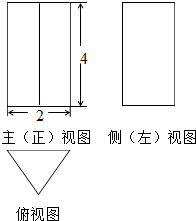

| A. | 4$\sqrt{3}$ | B. | $\frac{4}{3}$$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{3}$ |