题目内容
16.设二次函数f(x)=x2+ax+$\frac{{a}^{2}}{4}$+1(a∈R),求函数f(x)在[-1,1]上的最小值,g(a)的表达式.分析 求出二次函数的对称轴方程,讨论对称轴和区间[-1,1]的关系,运用函数的单调性即可得到最小值g(a)的表达式.
解答 解:f(x)=x2+ax+$\frac{{a}^{2}}{4}$+1=(x+$\frac{a}{2}$)2+1,对称轴为x=-$\frac{a}{2}$,
(1)若-$\frac{a}{2}$≥1,即a≤-2时,f(x)在[-1,1]上是减函数,∴g(a)=f(1)=$\frac{{a}^{2}}{4}$+a+2;
(2)若-1<-$\frac{a}{2}$<1,即-2<a<2时,f(x)在[-1,1]上先减后增,∴g(a)=f(-$\frac{a}{2}$)=1;
(3)若-$\frac{a}{2}$≤-1,即a>2时,f(x)在[-1,1]上增函数,∴g(a)=f(-1)=$\frac{{a}^{2}}{4}$-a+2.
综上可得,g(a)=$\left\{\begin{array}{l}{\frac{{a}^{2}}{4}+a+2,a≤-2}\\{1,-2<a<2}\\{\frac{{a}^{2}}{4}-a+2,a≥2}\end{array}\right.$.
点评 本题考查二次函数在闭区间上的最值的求法,考查不等式的性质和分类讨论的思想方法,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
6.某商店经营一批进价为每件4元的商品,在市场调查时发现,此商品的销售单价x与日销售量y之间有如下关系:
(1)求相关系数.并以此判断销售单价与日销售量之间具有怎样的线性相关关系?
(2)求x,y之间的线性回归方程;
(3)估计销售单价为多少元时,日利润最大?
(参考数据:$\sum_{i=1}^4{{x_i}{y_i}-4\overline x\overline y}$=-11,$\sum_{i=1}^4{x_i^2-4{{(\overline x)}^2}}$=5,$\sum_{i=1}^4{y_i^2-4{{(\overline y)}^2}}$=26)
用最小二乘法求线性回归方程系数公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$,r=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sqrt{\sum_{i=1}^{n}{x}_{i}^{2}-n(\overline{x})^{2}}\sqrt{\sum_{i=1}^{n}{y}_{i}^{2}-n(\overline{y})^{2}}}$.
| x | 5 | 6 | 7 | 8 |
| y | 10 | 8 | 7 | 3 |
(2)求x,y之间的线性回归方程;
(3)估计销售单价为多少元时,日利润最大?
(参考数据:$\sum_{i=1}^4{{x_i}{y_i}-4\overline x\overline y}$=-11,$\sum_{i=1}^4{x_i^2-4{{(\overline x)}^2}}$=5,$\sum_{i=1}^4{y_i^2-4{{(\overline y)}^2}}$=26)
用最小二乘法求线性回归方程系数公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$,r=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sqrt{\sum_{i=1}^{n}{x}_{i}^{2}-n(\overline{x})^{2}}\sqrt{\sum_{i=1}^{n}{y}_{i}^{2}-n(\overline{y})^{2}}}$.
11.把函数y=ex的图象按向量$\overrightarrow{a}$=(2,0)平移,得到y=f(x)的图象,则f(x)=( )
| A. | ex+2 | B. | ex-2 | C. | ex+2 | D. | ex-2 |
6.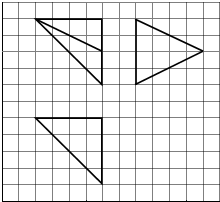 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )| A. | 8 | B. | $4\sqrt{5}$ | C. | 12 | D. | 16 |