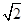题目内容
(本题满分14分)
在等差数列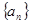 中,已知
中,已知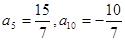 。
。
(Ⅰ)求通项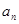 和前n项和
和前n项和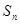 ;
;
(Ⅱ)求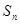 的最大值以及取得最大值时的序号
的最大值以及取得最大值时的序号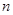 的值;
的值;
(Ⅲ)求数列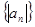 的前n项和
的前n项和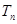 .
.
在等差数列
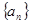 中,已知
中,已知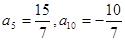 。
。(Ⅰ)求通项
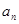 和前n项和
和前n项和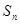 ;
;(Ⅱ)求
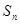 的最大值以及取得最大值时的序号
的最大值以及取得最大值时的序号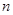 的值;
的值;(Ⅲ)求数列
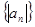 的前n项和
的前n项和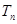 .
.(Ⅰ)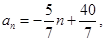
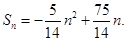 (Ⅱ)
(Ⅱ)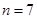 或
或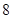 时
时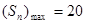
(Ⅲ)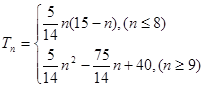
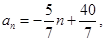
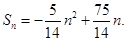 (Ⅱ)
(Ⅱ)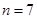 或
或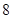 时
时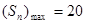
(Ⅲ)
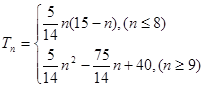
试题分析:(Ⅰ)设等差数列
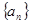 的公差为
的公差为 ,
,因为
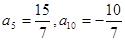 ,所以
,所以 ,所以
,所以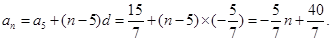 …2分
…2分又因为
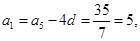 所以
所以 …4分
…4分(Ⅱ)

又因为
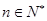 ,所以
,所以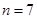 或
或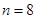 时,
时,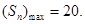 …9分
…9分(Ⅲ)
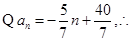 令
令 ,也就是
,也就是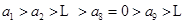 ,
,所以当
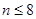 时,
时,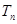 =
=
当
 时,
时,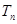 =
=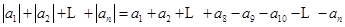
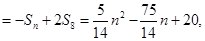
综上所述,数列
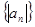 的前n项和
的前n项和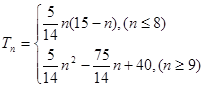 . …14分
. …14分 项和的计算,和前
项和的计算,和前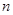 项和的最值的求法和带绝对值的数列的前
项和的最值的求法和带绝对值的数列的前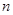 项和的计算,考查了学生的运算求解能力和分类讨论思想的应用.
项和的计算,考查了学生的运算求解能力和分类讨论思想的应用.点评:本题第(Ⅱ)问也可以令
 得
得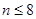 ,所以数列前7项或前8项的和最大,这是从数列的项的观点来求解,当然也可以从二次函数的观点来求解.第(Ⅲ)问中数列带绝对值,解题的关键是分清从第几项开始数列的项开始变号.
,所以数列前7项或前8项的和最大,这是从数列的项的观点来求解,当然也可以从二次函数的观点来求解.第(Ⅲ)问中数列带绝对值,解题的关键是分清从第几项开始数列的项开始变号.
练习册系列答案
相关题目
 满足
满足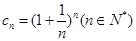 ,试证明:
,试证明: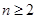 时,有
时,有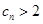 ;
;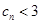 .
.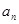 }中,
}中,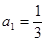 ,并且对任意
,并且对任意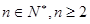 都有
都有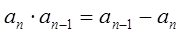 成立,令
成立,令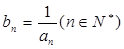 .
.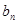 }的通项公式;
}的通项公式;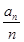 }的前n项和为
}的前n项和为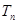 ,证明:
,证明: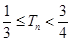
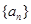 的前
的前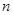 项和
项和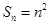 。(1)求数列
。(1)求数列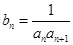 ,且数列
,且数列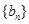 的前
的前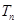 。若
。若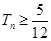 ,求
,求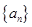 的前四项和为10,且
的前四项和为10,且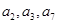 成等比数列
成等比数列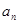
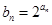 ,求数列
,求数列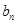 的前
的前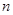 项和
项和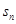
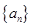 的通项公式为
的通项公式为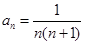 ,则该数列的前100项和为_________.
,则该数列的前100项和为_________.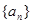 中,
中,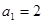 ,
,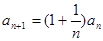 ,则
,则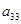 =________________
=________________