Question

【题目】已知函数f（x）=ax+ （其中a，b为常数）的图象经过（1，2），（2， ）两点．
（1）求函数f（x）的解析式；
（2）判断f（x）的奇偶性．

Answer 1

【答案】
（1）解：由已知有 ，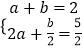

解得 ，

则f（x）=x+

（2）解：由题意f（x）的定义域为{x|x≠0}，关于原点对称，

又f（﹣x）=﹣x﹣ =﹣（x+ ）=﹣f（x），

∴f（x）是奇函数

【解析】（1）由条件可得a，b的方程组，解方程即可得到a，b，进而得到解析式；（2）运用奇偶性的定义，首先确定定义域是否关于原点对称，再计算f（﹣x），与f（x）比较，即可得到奇偶性．
【考点精析】解答此题的关键在于理解函数的奇偶性的相关知识，掌握偶函数的图象关于y轴对称；奇函数的图象关于原点对称．