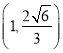题目内容
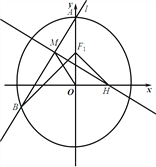
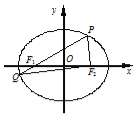
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,P为椭圆上一点(在x轴上方),连结PF1并延长交椭圆于另一点Q,设
(a>b>0)的左、右焦点分别为F1,F2,P为椭圆上一点(在x轴上方),连结PF1并延长交椭圆于另一点Q,设![]() =λ
=λ![]() .
.
(1)若点P的坐标为(1,![]() ),且△PQF2的周长为8,求椭圆C的方程;
),且△PQF2的周长为8,求椭圆C的方程;
(2)若PF2垂直于x轴,且椭圆C的离心率e∈[![]() ,
,![]() ],求实数λ的取值范围.
],求实数λ的取值范围.
【答案】(1)![]() +
+![]() =1;(2)[
=1;(2)[![]() ,5]
,5]
【解析】
试题分析:(1)求椭圆标准方程,实质就是要求![]() 的值,为此要找两个关于
的值,为此要找两个关于![]() 的方程,本题由已知,把
的方程,本题由已知,把![]() 点坐标代入可得一个方程,由椭圆定义知
点坐标代入可得一个方程,由椭圆定义知![]() 的周长是
的周长是![]() ,又可得
,又可得![]() 值,从而得解;(2)本小题关键是建立起
值,从而得解;(2)本小题关键是建立起![]() 与离心率
与离心率![]() 的关系,利用
的关系,利用![]() 两点在椭圆上,由
两点在椭圆上,由![]() 轴可求得
轴可求得![]() ,由
,由![]() =λ
=λ![]() ,可求得
,可求得![]() 点坐标,把
点坐标,把![]() 点坐标代入椭圆方程,再转化后可得
点坐标代入椭圆方程,再转化后可得![]() 的关系(λ2+4λ+3)e2=λ2-1,因为λ+1≠0,故有λ=
的关系(λ2+4λ+3)e2=λ2-1,因为λ+1≠0,故有λ=![]() ,从而可得
,从而可得![]() 的范围.
的范围.
试题解析:(1)因为F1,F2为椭圆C的两焦点,且P,Q为椭圆上的点,
所以PF1+PF2=QF1+QF2=2a,从而△PQF2的周长为4a.
由题意,得4a=8,解得a=2.
因为点P的坐标为(1,![]() ),所以
),所以![]() ,
,
解得b2=3.
所以椭圆C的方程为![]() .
.
(2)方法一:因为PF2⊥x轴,且P在x轴上方,故设P(c,y0),y0>0.设Q(x1,y1).
因为P在椭圆上,所以![]() ,解得y0=
,解得y0=![]() ,即P(c,
,即P(c,![]() ).
).
因为F1(-c,0),所以![]() =(-2c,-
=(-2c,-![]() ),
),![]() =(x1+c,y1).
=(x1+c,y1).
由![]() =λ
=λ![]() ,得-2c=λ(x1+c),-
,得-2c=λ(x1+c),-![]() =λy1,
=λy1,
解得x1=![]() ,y1=-
,y1=-![]() ,所以Q(-
,所以Q(-![]() c,-
c,-![]() ).
).
因为点Q在椭圆上,所以(![]() )2e2+
)2e2+![]() =1,
=1,
即(λ+2)2e2+(1-e2)=λ2,(λ2+4λ+3)e2=λ2-1,
因为λ+1≠0,
所以(λ+3)e2=λ-1,从而λ=![]() .
.
因为e∈[![]() ,
,![]() ],所以
],所以![]() ≤e2≤
≤e2≤![]() ,即
,即![]() ≤λ≤5.
≤λ≤5.
所以λ的取值范围为[![]() ,5].
,5].
方法二:因为PF2⊥x轴,且P在x轴上方,故设P(c,y0),y0>0.
因为P在椭圆上,所以![]() ,解得y0=
,解得y0=![]() ,即P(c,
,即P(c,![]() ).
).
因为F1(-c,0),故直线PF1的方程为![]() .
.
由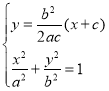 得(4c2+b2)x2+2b2cx+c2(b2-4a2)=0.
得(4c2+b2)x2+2b2cx+c2(b2-4a2)=0.
因为直线PF1与椭圆有一个交点为P(c,![]() ).设Q(x1,y1),
).设Q(x1,y1),
则x1+c![]() ,即-c-x1=
,即-c-x1=![]() .
.
因为![]() ,
,
所以λ=![]() =
=![]() .
.
因为e∈[![]() ,
,![]() ],所以
],所以![]() ≤e2≤
≤e2≤![]() ,即
,即![]() ≤λ≤5.
≤λ≤5.
所以λ的取值范围为[![]() ,5].
,5].

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】随着网络时代的进步,流量成为手机的附带品,人们可以利用手机随时随地的浏览网页,聊天,看视频,因此,社会上产生了很多低头族.某研究人员对该地区18∽50岁的5000名居民在月流量的使用情况上做出调查,所得结果统计如下图所示:
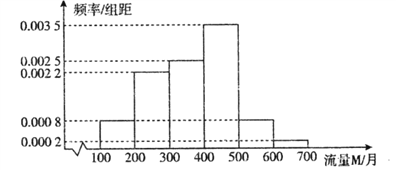
(Ⅰ)以频率估计概率,若在该地区任取3位居民,其中恰有![]() 位居民的月流量的使用情况
位居民的月流量的使用情况
在300M∽400M之间,求![]() 的期望
的期望![]() ;
;
(Ⅱ)求被抽查的居民使用流量的平均值;
(Ⅲ)经过数据分析,在一定的范围内,流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 成线性相关
成线性相关
关系,该研究人员将流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 的结果统计如下表所示:
的结果统计如下表所示:
折扣 | 1折 | 2折 | 3折 | 4折 | 5折 |
销售份数 | 50 | 85 | 115 | 140 | 160 |
试建立![]() 关于
关于![]() 的的回归方程.
的的回归方程.
附注:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
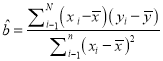 ,
, ![]()