جâؤ؟ؤعبف
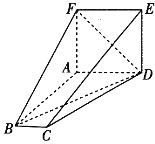
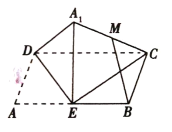
،¾جâؤ؟،؟ؤ³ر§ذ£¾ظذذضھت¶¾؛بü£¬µعز»آضر،°خ¹²ةèسذA،¢B،¢C،¢Dثؤ¸ِختج⣬¹وشٍبçدآ£؛
¢ظأ؟خ»²خ¼سصك¼ا·ضئ÷µؤ³ُت¼·ض¾ùخھ10·ض£¬´ً¶شختجâA،¢B،¢C،¢D·ض±ً¼س1·ض،¢2·ض،¢3·ض،¢6·ض£¬´ً´يبخز»جâ¼ُ2·ض£»
¢عأ؟»ط´ًز»ج⣬¼ا·ضئ÷دشت¾ہغ¼ئ·ضت£¬µ±ہغ¼ئ·ضتذ،سع8·ضت±£¬´ًجâ½لتّ£¬جشج³ِ¾ض£»µ±ہغ¼ئ·ضت´َسع»ٍµبسع14·ضت±£¬´ًجâ½لتّ£¬½ّبëدآز»آض£»µ±´ًحêثؤج⣬ہغ¼ئ·ضتبش²»×م14·ضت±£¬´ًجâ½لتّ£¬جشج³ِ¾ض£»
¢غأ؟خ»²خ¼سصك°´ختجâA،¢B،¢C،¢Dث³ذٍ×÷´ً£¬ض±ضء´ًجâ½لتّ£®
¼ظةè¼×ح¬ر§¶شختجâA،¢B،¢C،¢D»ط´ًصب·µؤ¸إآتزہ´خخھ![]() ،¢
،¢![]() ،¢
،¢![]() ،¢
،¢![]() £¬از¸÷جâ»ط´ًصب·سë·ٌد໥ض®¼نأ»سذس°دى£®
£¬از¸÷جâ»ط´ًصب·سë·ٌد໥ض®¼نأ»سذس°دى£®
£¨1£©اَ¼×ح¬ر§ؤـ½ّبëدآز»آضµؤ¸إآت£»
£¨2£©سأ¦خ±يت¾¼×ح¬ر§±¾آض´ًجâ½لتّت±´ًجâµؤ¸ِت£¬اَ¦خµؤ·ض²¼ءذ؛حتر§ئعحû¦¥¦خ£®
،¾´ً°¸،؟£¨1£©![]() £»£¨2£© ·ض²¼ءذ¼û½âخِ£¬ئعحûخھ
£»£¨2£© ·ض²¼ءذ¼û½âخِ£¬ئعحûخھ![]()
،¾½âخِ،؟
£¨1£©¸ù¾فجâز⣬ءذ¾ظ¼×ؤـ½ّبëدآز»آضµؤخهضضاé؟ِ£¬سةسعأ؟جâ´ًجâ½ل¹ûد໥¶ہء¢£¬¸ù¾فد໥¶شء¢تآ¼؛ح»¥³âتآ¼µؤ¸إآت¹«ت½£¬µأµ½½ل¹û£»
£¨2£©س´ح¼ز»؟ةضھ´ً¶شز»¸ِجâ»ٍ´ً´يز»¸ِجⶼ²»ؤـ¾ِ¶¨ؤم¼×µؤب¥ءô£¬ثùزش×îةظ´ًء½¸ِج⣬ثو»ْ±نء؟![]() ؟ةؤـµؤب،ضµخھ
؟ةؤـµؤب،ضµخھ![]() £¬سةسعأ؟جâµؤ´ًجâ½ل¹¹¶¼تادà¶ش¶ہء¢µؤ£¬¸ù¾فد໥¶شء¢تآ¼ح¬ت±·¢ةْµؤ¸إآتµأµ½½ل¹û£®
£¬سةسعأ؟جâµؤ´ًجâ½ل¹¹¶¼تادà¶ش¶ہء¢µؤ£¬¸ù¾فد໥¶شء¢تآ¼ح¬ت±·¢ةْµؤ¸إآتµأµ½½ل¹û£®
ةè![]() ·ض±ًتاµعز»،¢¶،¢ب،¢ثؤ¸ِختج⣬سأ
·ض±ًتاµعز»،¢¶،¢ب،¢ثؤ¸ِختج⣬سأ![]() ±يت¾¼×ح¬ر§µع
±يت¾¼×ح¬ر§µع![]() ¸ِختجâ»ط´ًصب·£¬سأ
¸ِختجâ»ط´ًصب·£¬سأ![]() ±يت¾µع
±يت¾µع![]() ¸ِختجâ»ط´ً´يخَ£¬شٍ
¸ِختجâ»ط´ً´يخَ£¬شٍ![]() تا¶شء¢تآ¼£¬
تا¶شء¢تآ¼£¬
سةجâزâµأ£¬![]() ,
,
شٍ![]() £¬
£¬
£¨1£©¼ا،°¼×ح¬ر§ؤـ½ّبëدآز»آض،±خھتآ¼Q£¬
شٍ![]()
![]()
![]() £®
£®
£¨2£©سةجâز⣬؟ةضھثو»ْ±نء؟![]() ؟ةؤـµؤب،ضµ
؟ةؤـµؤب،ضµ![]() £¬
£¬
سةسعأ؟جâ´ًجâ½ل¹û¶¼تادà¶ش¶شء¢µؤ£¬
زٍخھ![]() ,
,
![]()
![]() ,
,
| 2 | 3 | 4 |
|
|
|
|
ثùزش![]() £®
£®

 أûذ£ح¨ذذض¤سذذ§×÷زµدµءذ´ً°¸
أûذ£ح¨ذذض¤سذذ§×÷زµدµءذ´ً°¸،¾جâؤ؟،؟´سز»إْئ»¹ûضذ£¬ثو»ْ³éب،50¸ِ£¬ئنضطء؟£¨µ¥خ»£؛؟ث£©µؤئµت·ض²¼±يبçدآ£؛
·ض×飨ضطء؟£© |
|
|
|
|
ئµت£¨¸ِ£© | 5 | 10 | 20 | 15 |
(1) ¸ù¾فئµت·ض²¼±ي¼ئثمئ»¹ûµؤضطء؟شع![]() µؤئµآت£»
µؤئµآت£»
(2) سأ·ض²م³éرùµؤ·½·¨´سضطء؟شع![]() ؛ح
؛ح![]() µؤئ»¹ûضذ¹²³éب،4¸ِ£¬ئنضذضطء؟شع
µؤئ»¹ûضذ¹²³éب،4¸ِ£¬ئنضذضطء؟شع![]() µؤسذ¼¸¸ِ£؟
µؤسذ¼¸¸ِ£؟
(3) شع£¨2£©ضذ³é³ِµؤ4¸ِئ»¹ûضذ£¬بخب،2¸ِ£¬اَضطء؟شع![]() ؛ح
؛ح![]() ضذ¸÷سذ1¸ِµؤ¸إآت£®
ضذ¸÷سذ1¸ِµؤ¸إآت£®
،¾جâؤ؟،؟ؤ³تذخھءثءث½âأٌضع¶ش؟ھص¹´´½¨خؤأ÷³اتذ¹¤×÷زشہ´µؤآْزâ¶ب£¬ثو»ْµ÷²éءث40أûب؛ضع£¬²¢½«ثûأاثو»ْ·ض³ة![]() £¬
£¬![]() ء½×飬أ؟×é20بث£¬
ء½×飬أ؟×é20بث£¬![]() ×éب؛ضع¸ّµعز»½×¶خµؤ´´خؤ¹¤×÷ئہ·ض£¬
×éب؛ضع¸ّµعز»½×¶خµؤ´´خؤ¹¤×÷ئہ·ض£¬![]() ×éب؛ضع¸ّµع¶½×¶خµؤ´´خؤ¹¤×÷ئہ·ض£¬¸ù¾فء½×éب؛ضعµؤئہ·ض»وضئءثبçح¼ثùت¾µؤ¾¥ز¶ح¼.
×éب؛ضع¸ّµع¶½×¶خµؤ´´خؤ¹¤×÷ئہ·ض£¬¸ù¾فء½×éب؛ضعµؤئہ·ض»وضئءثبçح¼ثùت¾µؤ¾¥ز¶ح¼.
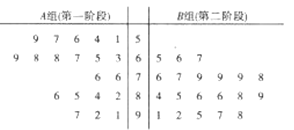
£¨¢ٌ£©¸ù¾ف¾¥ز¶ح¼±ب½دب؛ضع¶شء½¸ِ½×¶خµؤ´´خؤ¹¤×÷آْزâ¶بئہ·ضµؤئ½¾ùضµ؛ح¼¯ضذ³ج¶ب£¨²»زھاَ¼ئثم³ِ¾كجهضµ£¬¸ّ³ِ½لآغ¼´؟ة£©£»
£¨¢ٍ£©حê³ةدآأوµؤءذءھ±ي£¬²¢ح¨¹¼ئثمإذ¶دتا·ٌسذ![]() µؤ°رخصبدخھأٌضع¶شء½¸ِ½×¶خ´´خؤ¹¤×÷µؤآْزâ¶ب´وشع²îزى£؟
µؤ°رخصبدخھأٌضع¶شء½¸ِ½×¶خ´´خؤ¹¤×÷µؤآْزâ¶ب´وشع²îزى£؟
µحسع70·ض | ²»µحسع70·ض | ؛د¼ئ | |
µعز»½×¶خ | |||
µع¶½×¶خ | |||
؛د¼ئ |
²خ؟¼¹«ت½£؛![]() £¬
£¬![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |