Question

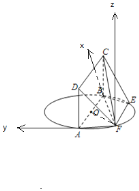
【题目】如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面与圆O所在的平面互相垂直．已知AB＝2，EF＝1．

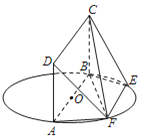
（Ⅰ）求证：平面DAF⊥平面CBF；

（Ⅱ）当AD＝1时，求直线FB与平面DFC所成角的正弦值．

Answer 1

【答案】（Ⅰ）证明见解析（Ⅱ）．

【解析】

(Ⅰ)证明BF⊥平面ADF即可.

(Ⅱ) 以F为原点建立空间直角坐标系,再根据空间向量的方法求解直线FB与平面DFC所成角的正弦值即可.

（Ⅰ）证明：∵AB为圆O的直径,点E、F在圆O上,∴AF⊥BF,

∵矩形ABCD所在的平面与圆O所在的平面互相垂直,

∴AD⊥AB,∴AD⊥平面ABEF,∴AD⊥BF,

∵AD∩AF＝A,∴BF⊥平面ADF,

∵BF平面CBF,∴平面DAF⊥平面CBF．

（Ⅱ）解：连结FO,∵AB＝2,EF＝1,AB∥EF,

∴当AD＝1时,四边形EFOB是菱形,

以F为原点,FB为x轴,FA为y轴,过F作平面ABEF的垂线为z轴,建立空间直角坐标系,

F（0,0,0）,B（,0,0）,C（,0,1）,D（0,1,1）,

（,0,0）,（,0,1）,（0,1,1）,

设平面DFC的法向量（x,y,z）,

则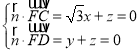,取x＝1,得（1,,）,

设直线FB与平面DFC所成角为θ,

则sinθ．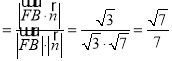

∴直线FB与平面DFC所成角的正弦值为．