题目内容
【题目】已知正三角形
的边长为3，
分别是
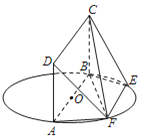
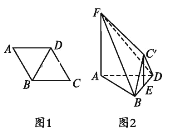
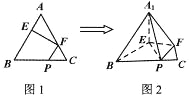
边上的点，满足
(如图1)．将
折起到
的位置，使平面
平面
，连接
(如图2)．
(1)求证：
平面 ；
(2)求二面角
的余弦值．
【答案】(1)见证明；(2) 
【解析】
（1）在图
中，取
的中点
，连接
，证明
是等边三角形，由此证得
，即在图
中有
，根据面面垂直的性质定理可证得
平面
.（2）以
为原点，以向量
的方向为
轴的正方向建立空间直角坐标系，利用平面
的法向量和
的法向量，计算二面角的余弦值.
解：（1）在图1中，取BE的中点D，连结DF．
∵
，
∴
.
而
，∴是正三角形．
又
，∴
即在图2中，，
∵平面
平面，平面
平面
，
平面.
（2）由（1）知，即平面，
．
以E为原点，以向量的方向为轴的正方向建立如图所示的坐标系，
则
.
.
设
分别是平面
和平面
的法向量，
由
，得
，
取
，得
，
由
，得
，
取
，得
，
所以
.
因为二面角
为钝角，所以二面角的余弦值为
.
练习册系列答案
相关题目
【题目】（1）某校夏令营有3名男同学A、B、C和3名女同学X、Y、Z，其年级情况如下表：
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)．
①用表中字母列举出所有可能的结果；
②设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”，求事件M发生的概率．
（2）节日前夕，小李在家门前的树上挂了两串彩灯．这两串彩灯的第一次闪亮相互独立，且都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以4秒为间隔闪亮．那么这两串彩灯同时通电后，它们第一次闪亮的时刻相差不超过2秒的概率是多少？
