题目内容
1．已知函数f（x）=kx-$\frac{k}{x}$-2lnx在定义域单调递增，求k的取值范围．分析 先求f′（x），由于函数f（x）=kx-$\frac{k}{x}$-2lnx在定义域单调递增，可得f′（x）≥0在函数的定义域上恒成立，解出即可．
解答 解：由于函数f（x）=kx-$\frac{k}{x}$-2lnx的定义域为（0，+∞），
则f′（x）=k+k•$\frac{1}{{x}^{2}}$-$\frac{2}{x}$=$\frac{1}{{x}^{2}}$（kx2-2x+k）（x＞0），
∵函数f（x）=kx-$\frac{k}{x}$-2lnx在定义域单调递增，
∴f′（x）≥0，即kx2-2x+k≥0在区间（0，+∞）上恒成立．
∴$\left\{\begin{array}{l}{k＞0}\\{△≤0}\end{array}\right.$或$\left\{\begin{array}{l}{k＞0}\\{△＞0}\\{f（0）≥0}\end{array}\right.$，解得k≥1或0＜k＜1，
∴k＞0，
∴k的取值范围是（0，+∞）．
点评 本题考查了利用导数研究函数的单调性、恒成立问题的等价转化方法，属于中档题．
练习册系列答案
相关题目
11．已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）与直线y=2x有交点，则双曲线离心率的取值范围是（ ）
| A． | （$\sqrt{5}$，+∞） | B． | [$\sqrt{5}$，+∞） | C． | （1，$\sqrt{5}$）∪（$\sqrt{5}$，+∞） | D． | （1，$\sqrt{5}$） |
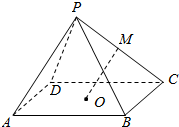如图，在四棱锥P-ABCD中，底面是正方形，中心为O，且底面边长和侧棱长相等，M是PC的中点，求MO与AB所成的角．