题目内容
为了解某校学生参加某项测试的情况，从该校学生中随机抽取了6位同学，这6位同学的成绩(分数)如茎叶图所示.
⑴求这6位同学成绩的平均数和标准差;
⑵从这6位同学中随机选出两位同学来分析成绩的分布情况，设
为这两位同学中成绩低于平均分的人数，求的分布列和期望.
⑴这6位同学的成绩平均数为81；标准差为7；
⑵的分布列为0 1 2 P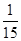 
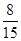
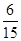
的数学期望为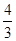
.
解析试题分析：⑴代入平均数及标准差的公式即得；⑵由（1）可得平均分为81，所以低于平均分的有4人，现从中抽取2人，随机变量可能的取值为0,1,2.这是一个超几何分布，由超几何分布的概率公式即可得其分布列及期望.
试题解析：⑴这6位同学的成绩平均数为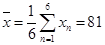
.
又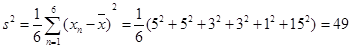
.
故这6位问学成绩的标准差为s=7 .6分
⑵随机变量可能的取值为0,1,2，则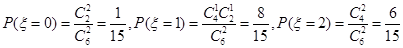
.
故的分布列为0 1 2 P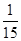 
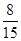
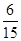
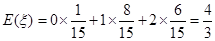
即的数学期望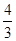 12分
考点：1、平均数与标准差；2、随机变量的分布列及期望；3、超几何分布.
练习册系列答案
手拉手全优练考卷系列答案
相关题目
空气质量指数PM2.5(单位：μg/m3)表示每立方米空气中可入肺颗粒物的含量，这个值越高，解代表空气污染越严重：
| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
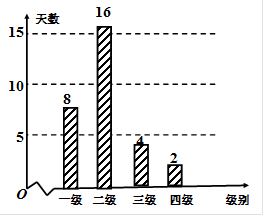
某市2013年3月8日—4月7日(30天)对空气质量指数PM2.5进行检测，获得数据后整理得到如下条形图：
(1)估计该城市一个月内空气质量类别为良的概率；
(2)从空气质量级别为三级和四级的数据中任取2个，求至少有一天空气质量类别为中度污染的概率.
为了对新产品进行合理定价，对该产品进行了试销试验，以观察需求量Y(单位：千件)对于价格x(单位：千元)的反应，得数据如下：
| x/千元 | 50 | 70 | 80 | 40 | 30 | 90 | 95 | 97 |
| y/千件 | 100 | 80 | 60 | 120 | 135 | 55 | 50 | 48 |
(2)若成本x＝y＋500，试求：
①在盈亏平衡条件下(利润为零)的价格；
②在利润为最大的条件下，定价为多少？
想象一下一个人从出生到死亡，在每个生日都测量身高，并作出这些数据的散点图，这些点将不会落在一条直线上，但在一段时间内的增长数据有时可以用线性回归来分析，下表是一位母亲给儿子做的成长记录：
| 年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 91.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| | |||||||
| 年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
(2)如果年龄相差5岁，则身高有多大差异(3～16岁之间)?
(3)如果身高相差20 cm，其年龄相差多少(3～16岁之间)?
(4)计算残差，说明该函数模型是否能够较好地反映年龄与身高的关系，说明理由．
下表是对某市8所中学学生是否吸烟进行调查所得的结果：
| | 吸烟学生 | 不吸烟学生 |
| 父母中至少有一人吸烟 | 816 | 3 203 |
| 父母均不吸烟 | 188 | 1 168 |
(2)在父母均不吸烟的学生中，估计吸烟学生所占的百分比是多少？
(3)学生的吸烟习惯和父母是否吸烟有关吗？请简要说明理由．
(4)有多大的把握认为学生的吸烟习惯和父母是否吸烟有关？
表示.
，求
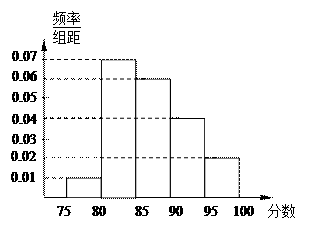
、抽测成绩的中位数及分数分别在
，
内的人数；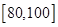
内的学生中任选两人进行调研谈话，求恰好有一人分数在