题目内容
想象一下一个人从出生到死亡，在每个生日都测量身高，并作出这些数据的散点图，这些点将不会落在一条直线上，但在一段时间内的增长数据有时可以用线性回归来分析，下表是一位母亲给儿子做的成长记录：
| 年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 91.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| | |||||||
| 年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
(2)如果年龄相差5岁，则身高有多大差异(3～16岁之间)?
(3)如果身高相差20 cm，其年龄相差多少(3～16岁之间)?
(4)计算残差，说明该函数模型是否能够较好地反映年龄与身高的关系，说明理由．
(1)
＝6.286x＋72 (2) 31.4 cm (3) 3(岁) (4) 拟合效果较好
解析解：(1)设年龄x与身高y之间的回归直线方程为 为了了解调研高一年级新学生的智力水平，某校按l 0％的比例对700名高一学生按性别分别进行“智力评分”抽样检查，测得“智力评分”的频数分布表如下表l，表2． 户外运动已经成为一种时尚运动，某单位为了了解员工喜欢户外运动是否与性别有关，决定从本单位全体650人中采用分层抽样的办法抽取50人进行问卷调查，得到了如下列联表： 有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次.根据年龄将大众评委分为五组,各组的人数如下:＝
x＋
，由公式＝
得≈6.286，＝
－
≈72，所以＝6.286x＋72.
(2)如果年龄相差5岁，则预报变量变化6.286×5＝31.425，即身高相差约31.4 cm.
(3)如果身高相差20 cm，年龄相差Δx＝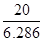
＝3.182≈3(岁)．
(4)y 91.8 97.6 104.2 110.9 115.6 122.0 128.5 i90.9 97.1 103.4 109.7 116.0 122.3 128.6 y 134.2 140.8 147.6 154.2 160.9 167.5 173.0 i134.9 
表1：男生“智力评分”频数分布表智力评分
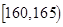
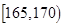
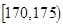
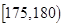
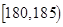
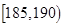
频数
2
5
14
13
4
2
表2：女生“智力评分”频数分布表智力评分
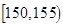
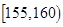
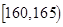
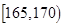
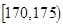
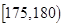
频数
1
7
12
6
3
1
（1）求高一的男生人数并完成下面男生的频率分布直方图；
（2）估计该校学生“智力评分”在[1 65，1 80）之间的概率；
（3）从样本中“智力评分”在[180，190）的男生中任选2人，求至少有1人“智力评分”在[185，190）之间的概率．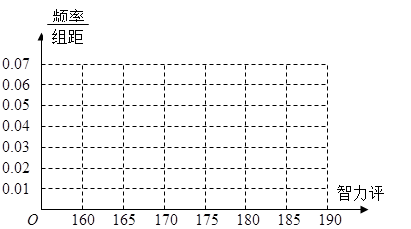
已知在这50人中随机抽取1人抽到喜欢户外运动的员工的概率是 喜欢户外运动 不喜欢户外运动 合计 男性 5 女性 10 合计 50 
.
(1)请将上面的列联表补充完整；(2)求该公司男、女员工各多少名；
(3)是否有
的把握认为喜欢户外运动与性别有关？并说明你的理由．
下面的临界值表仅供参考：
参考公式：
0.15 0.10 0.05 0.025 0.010 0.005 0.001 
2.072 2.706 3.841 5.024 6.635 7.879 10.828 
，其中
.
(1)为了调查评委对7位歌手的支持状况,现用分层抽样方法从各组中抽取若干评委,其中从B组抽取了6人.请将其余各组抽取的人数填入下表.组别
A
B
C
D
E
人数
50
100
150
150
50
(2)在(1)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率. 组别
A
B
C
D
E
人数
50
100
150
150
50
抽取人数
6
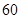名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过
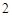千元的顾客被定义为“网购红人”,网购金额不超过
.
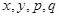的值,并补全频率分布直方图(图(2)).
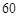名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
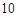人,若需从这
人进行问卷调查,设
为选取的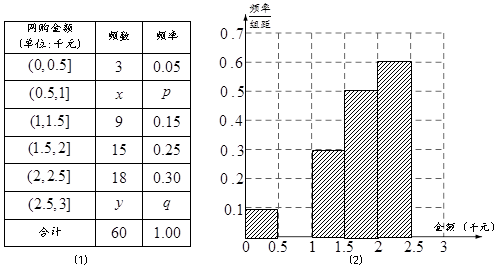
为这两位同学中成绩低于平均分的人数，求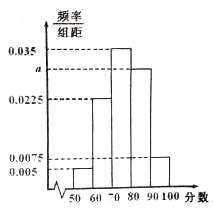
技术规定》 （试行），
为优，
为良，
为轻度污染，
为中度污染，
，
均为重度污染，
及以上为严重污染．某市2013年11月份
天的
天进行市民户外晨练人数调查，则中度污染被抽到的天数共有多少天？
时市民适宜户外晨练，若市民王先生决定某天早晨进行户外晨练，则他当天适宜户外晨练的概率是多少？