题目内容
参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题:
(1)求参加数学抽测的人数 、抽测成绩的中位数及分数分别在
、抽测成绩的中位数及分数分别在 ,
, 内的人数;
内的人数;
(2)若从分数在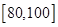 内的学生中任选两人进行调研谈话,求恰好有一人分数在
内的学生中任选两人进行调研谈话,求恰好有一人分数在 内的概率.
内的概率.
(1)参加数学竞赛人数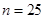 ,中位数为73,分数在
,中位数为73,分数在 、
、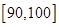 内的人数分别为
内的人数分别为 人、
人、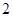 人.
人.
(2)恰好有一人分数在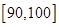 内的概率为
内的概率为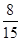 .
.
解析试题分析:(1)注意应用频率分布直方图中矩形的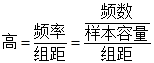 ,
, 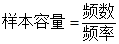 ;
;
(2)设“在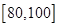 内的学生中任选两人,恰好有一人分数在
内的学生中任选两人,恰好有一人分数在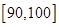 内”为事件
内”为事件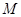 ,
,
将 内的
内的 人编号为
人编号为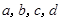 ;
;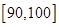 内的
内的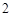 人编号为
人编号为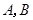
在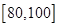 内的任取两人的基本事件为:
内的任取两人的基本事件为: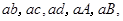
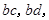
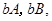
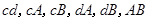 共15个,其中,恰好有一人分数在
共15个,其中,恰好有一人分数在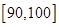 内的基本事件有
内的基本事件有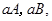
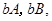
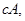
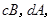
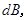 共8个.
共8个.
由古典概型概率的计算公式即得所求.
试题解析:(1)分数在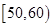 内的频数为2,由频率分布直方图可以看出,分数在
内的频数为2,由频率分布直方图可以看出,分数在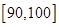 内同样有
内同样有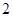 人. 2分,
人. 2分,
由 , 得
, 得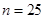 , 3分
, 3分
茎叶图可知抽测成绩的中位数为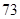 . 4分
. 4分 分数在
分数在 之间的人数为
之间的人数为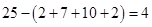 5分
5分
参加数学竞赛人数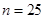 ,中位数为73,分数在
,中位数为73,分数在 、
、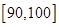 内的人数分别为
内的人数分别为 人、
人、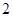 人. 6分
人. 6分
(2)设“在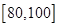 内的学生中任选两人,恰好有一人分数在
内的学生中任选两人,恰好有一人分数在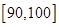 内”为事件
内”为事件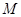 ,
,
将 内的
内的 人编号为
人编号为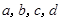 ;
;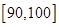 内的
内的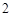 人编号为
人编号为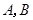
在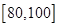 内的任取两人的基本事件为:
内的任取两人的基本事件为: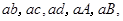
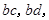
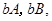
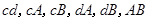 共15个 9分
共15个 9分
其中,恰好有一人分数在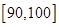 内的基本事件有
内的基本事件有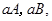
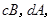
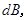

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0 16 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0 40 |
| 第4组 | [80,90) | ▓ | 0 08 |
| 第5组 | [90,100] | 2 | b |
| | 合计 | ▓ | ▓ |

(1)求出
 的值;
的值;(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动
(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率;
(ⅱ)求所抽取的2名同学来自同一组的概率
有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次.根据年龄将大众评委分为五组,各组的人数如下:
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 抽取人数 | | 6 | | | |
某地粮食需求量逐年上升,下表是部分统计数据:
| 年份(年) | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量 (万吨) | 236 | 246 | 257 | 276 | 286 |
 =
= x+
x+ .
.(2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量.
城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的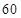 名候车乘客中随机抽取
名候车乘客中随机抽取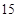 人,将他们的候车时间作为样本分成
人,将他们的候车时间作为样本分成 组,如下表所示(单位:min):
组,如下表所示(单位:min):
| 组别 | 候车时间 | 人数 |
| 一 |  |  |
| 二 |  | 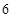 |
| 三 |  |  |
| 四 |  |  |
| 五 |  |  |
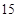 名乘客的平均候车时间;
名乘客的平均候车时间;(2)估计这
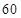 名乘客中候车时间少于
名乘客中候车时间少于 分钟的人数;
分钟的人数;(3)若从上表第三、四组的
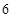 人中选
人中选 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率. 
 为这两位同学中成绩低于平均分的人数,求
为这两位同学中成绩低于平均分的人数,求

 ,求恰有一名同学获得该高校B类资格的概率.
,求恰有一名同学获得该高校B类资格的概率.