Question

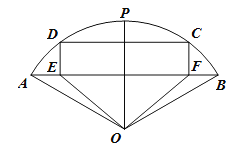
【题目】有一块圆心角为120度，半径为的扇形钢板(为弧的中点)，现要将其裁剪成一个五边形磨具，其下部为等腰三角形，上部为矩形.设五边形的面积为.

（1）写出关于的函数表达式，并写出的取值范围；

（2）当取得最大值时，求的值.

Answer 1

【答案】(1) S＝R2sinα（4cosα－1）（0＜α＜）(2)

【解析】

(1)根据直角三角形解得矩形的长与宽以及等腰三角形的底与高，再根据矩形面积公式以及三角形面积公式求结果，最后根据实际意义确定的取值范围；(2)利用导数求函数最值.

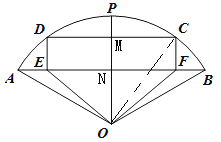
（1）如图，设OP与CD、AB交于M，N两点，

为弧的中点，则M为CD中点，OP⊥AB，

OM＝OCcosα＝Rcosα，CM＝OCsinα=Rsinα，则EF＝CD＝2CM＝2Rsinα

∠POB＝∠AOB＝60°，∠OBN＝30°，

所以，ON＝OB＝R，

CF＝MN＝OM－ON＝Rcosα－R

所以，S＝CDCF+EFON＝2Rsinα×（Rcosα－R）+×2Rsinα×R

　　　　＝R2sinα（4cosα－1）（0＜α＜）

（2）设f（α）＝sinα（4cosα－1），则

＝＝0

因为0＜α＜，所以，

由表可，当S取得最大值时，