题目内容
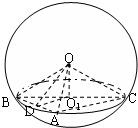 如图,已知A,B,C是表面积为48π的球面上的三点,AB=2,BC=4,∠ABC=60°,O为球心,则二面角O-AB-C的大小为:( )
如图,已知A,B,C是表面积为48π的球面上的三点,AB=2,BC=4,∠ABC=60°,O为球心,则二面角O-AB-C的大小为:( )A、
| ||||
B、
| ||||
C、arccos
| ||||
D、arccos
|
分析:先求出球的半径,BC的中点为O1,取AB中点D,连OD、O1D,则∠ODO1是二面角O-AB-C的平面角,在Rt△OO1D中求出此角即可.
解答:解:球的半径为2
;△ABC为直角三角形,斜边BC是其外接圆的直径,
记BC的中点为O1,则OO1⊥面ABC,在Rt△OO1B中,OB=2
,BO1=2,
∴OO1=2
;取AB中点D,连OD、O1D,则AB⊥OD,AB⊥O1D,
∴∠ODO1是二面角O-AB-C的平面角,在Rt△ABC中O1D=
AC=
故在Rt△OO1D中,OD=
,cos∠ODO1=
,∴∠ODO1=arccos
,
故选D.
| 3 |
记BC的中点为O1,则OO1⊥面ABC,在Rt△OO1B中,OB=2
| 3 |
∴OO1=2
| 2 |
∴∠ODO1是二面角O-AB-C的平面角,在Rt△ABC中O1D=
| 1 |
| 2 |
| 3 |
故在Rt△OO1D中,OD=
| 11 |
| ||
|
| ||
| 11 |
故选D.
点评:本小题主要考查球的表面积以及二面角的平面角及求法等有关知识,同时考查空间想象能力,计算能力,属于中档题.

练习册系列答案
相关题目
 17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|=
17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|= 如图,已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|等于( )
如图,已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|等于( ) 如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC.
如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC. 如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且
如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且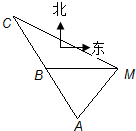 (2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )
(2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )