题目内容
 17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|=
17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|=1
.分析:先看当直线斜率不存在时,直线方程可得,进而可直接求得A,B,C,D的坐标,则利用两点间的距离公式求得AB,CD则答案可得;当直线斜率存在时,设出直线方程与抛物线方程联立利用韦达定理求得xaxb,根据抛物线的焦点F同时是已知圆的圆心,根据抛物线的定义可求得|AB|=|AF|-|BF|=xa,|CD|=|DF|-|CF|=xb.最后根据xaxb的值求得答案.
解答:解:若直线的斜率不存在,则直线方程为x=1,代入抛物线方程和圆的方程,
可直接得到ABCD四个点的坐标为(1,2)(1,1)(1,-1)(1,-2),
所以AB=1,CD=1,
从而|AB•CD|=1.
若直线的斜率存在,设为k,则直线方程为y=k(x-1),因为直线过抛物线的焦点(1,0)
不妨设A(xa,ya),B(xb,yb),过AB分别作抛物线准线的垂线,由抛物线的定义,
|AF|=xa+1,|DF|=xb+1,
把直线方程与抛物线方程联立,消去y可得
k2x2-(2k2+4)x+k2=0,由韦达定理有 xaxb=1
而抛物线的焦点F同时是已知圆的圆心,所以|BF|=|CF|=R=1
从而有|AB|=|AF|-|BF|=xa,|CD|=|DF|-|CF|=xb.
所以|AB•CD|=xaxb=1
故答案为:1
可直接得到ABCD四个点的坐标为(1,2)(1,1)(1,-1)(1,-2),
所以AB=1,CD=1,
从而|AB•CD|=1.
若直线的斜率存在,设为k,则直线方程为y=k(x-1),因为直线过抛物线的焦点(1,0)
不妨设A(xa,ya),B(xb,yb),过AB分别作抛物线准线的垂线,由抛物线的定义,
|AF|=xa+1,|DF|=xb+1,
把直线方程与抛物线方程联立,消去y可得
k2x2-(2k2+4)x+k2=0,由韦达定理有 xaxb=1
而抛物线的焦点F同时是已知圆的圆心,所以|BF|=|CF|=R=1
从而有|AB|=|AF|-|BF|=xa,|CD|=|DF|-|CF|=xb.
所以|AB•CD|=xaxb=1
故答案为:1
点评:本题主要考查了抛物线的简单性质,直线与抛物线的关系.在设直线的方程的时候,一定要对直线的斜率的存在情况进行分类讨论.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图,已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|等于( )
如图,已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|等于( ) 如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC.
如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC. 如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且
如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且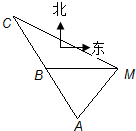 (2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )
(2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )