题目内容
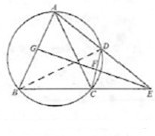
 如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC.
如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC.(1)证明:AB2=AD•AE;
(2)若EG平分∠AEB,且与AB、CD分别相交于点G、F,证明:∠CFG=∠BGF.
分析:(1)连接BD,由AB=AC,知∠ABC=∠ADB,由∠BAD=∠EAB,知△ABD∽△AEB,由此能证明AB2=AD•AE.
(2)由A、B、C、D四点共圆,知∠ABC=∠EDF,由∠DEF=∠BEG,能证明∠CFG=∠BGF.
(2)由A、B、C、D四点共圆,知∠ABC=∠EDF,由∠DEF=∠BEG,能证明∠CFG=∠BGF.
解答:证明:(1)如图,连接BD,
∵AB=AC,∴∠ABC=∠ADB,
∵∠BAD=∠EAB,
∴△ABD∽△AEB,
∴
=
,
∴AB2=AD•AE.
(2)∵A、B、C、D四点共圆,
∴∠ABC=∠EDF,
∵EG平分∠AEB,∴∠DEF=∠BEG,
∴∠EGB=∠EFD,
∵∠CFG=∠EFD,∠EGB=∠BGF,
∴∠CFG=∠BGF.
∵AB=AC,∴∠ABC=∠ADB,
∵∠BAD=∠EAB,
∴△ABD∽△AEB,
∴
| AB |
| AD |
| AE |
| AB |
∴AB2=AD•AE.
(2)∵A、B、C、D四点共圆,
∴∠ABC=∠EDF,
∵EG平分∠AEB,∴∠DEF=∠BEG,
∴∠EGB=∠EFD,
∵∠CFG=∠EFD,∠EGB=∠BGF,
∴∠CFG=∠BGF.

点评:本题考查与圆有关的比例线段的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|=
17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|= 如图,已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|等于( )
如图,已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|等于( ) 如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且
如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且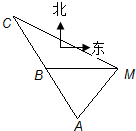 (2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )
(2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )