题目内容
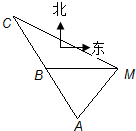（2009•台州二模）如图，已知A、B、C是一条直路上的三点，一个人从A出发行走到B处时，望见塔M（将塔M视为与A、B、C在同一水平面上一点）在正东方向且A在东偏南α方向，继续行走1km在到达C处时，望见塔M在东偏南β方向，则塔M到直路ABC的最短距离为（ ）分析：过M作MN⊥AB，交AB于点N，根据题意得：∠BMC=β，∠ABM=α，利用外角性质得到∠C=α-β，在三角形BCM中，利用正弦定理表示出BM，在直角三角形BMN中，利用锐角三角函数定义表示出MN，即为塔M到直路ABC的最短距离．
解答：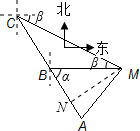
解：过M作MN⊥AB，交AB于点N，
根据题意得：∠BMC=β，∠ABM=α，
∴∠C=α-β，
在△BCM中，由正弦定理得：
=
，
∴BM=
km，
在Rt△BMN中，MN=BMsinα=
km．
故选B
解：过M作MN⊥AB，交AB于点N，根据题意得：∠BMC=β，∠ABM=α，
∴∠C=α-β，
在△BCM中，由正弦定理得：
| 1 |
| sinβ |
| BM |
| sin(α-β) |
∴BM=
| sin(α-β) |
| sinβ |
在Rt△BMN中，MN=BMsinα=
| sinαsin(α-β) |
| sinβ |
故选B
点评：此题考查了正弦定理，以及锐角三角函数定义，熟练掌握正弦定理是解本题的关键．
练习册系列答案
相关题目
