题目内容
 如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且
如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且| AC |
| BC |
| BC |
| AC |
(1)求椭圆的标准方程;
(2)若过C关于y轴对称的点D作椭圆的切线DE,则AB与DE有什么位置关系?证明你的结论.
分析:(1)设所求椭圆的方程为:
+
=1(0<b<2),由椭圆的对称性知,|OC|=|OB|,由
•
=0,AC⊥BC.|BC|=2|AC|,|OC|=|AC|,知△AOC是等腰直角三角形,由此能够求出椭圆方程.
(2)设所求切线方程为y-1=k(x+1),由
,消去x,(1+3k2)x2+6k(k+1)x+3(k+1)2-4=0,由判别式等于0,能判断AB与DE平行.
| x2 |
| 4 |
| y2 |
| b2 |
| AC |
| BC |
(2)设所求切线方程为y-1=k(x+1),由
|
解答:解:(1)A(2,0),
设所求椭圆的方程为:
+
=1(0<b<2),…(2分)
由椭圆的对称性知,
|OC|=|OB|,
由
•
=0,AC⊥BC.
∵|BC|=2|AC|,
∴|OC|=|AC|,
∴△AOC是等腰直角三角形,
∴C是坐标为(1,1).…(4分)
∵C点在椭圆上,
∴
+
=1,
∴b2=
.
所求的椭圆方程为
+
=1.…(8分)
(2)AB与DE是平行关系…(10分)
D(-1,1),
设所求切线方程为y-1=k(x+1),
,消去x,(1+3k2)x2+6k(k+1)x+3(k+1)2-4=0…(12分)
上述方程中判别式△=9k2-6k+1=0,k=
又kAB=
,
所以AB与DE平行…(14分)
设所求椭圆的方程为:
| x2 |
| 4 |
| y2 |
| b2 |
由椭圆的对称性知,
|OC|=|OB|,
由
| AC |
| BC |
∵|BC|=2|AC|,
∴|OC|=|AC|,
∴△AOC是等腰直角三角形,
∴C是坐标为(1,1).…(4分)
∵C点在椭圆上,
∴
| 12 |
| 4 |
| 1 |
| b2 |
∴b2=
| 4 |
| 3 |
所求的椭圆方程为
| x2 |
| 4 |
| 3y2 |
| 4 |
(2)AB与DE是平行关系…(10分)
D(-1,1),
设所求切线方程为y-1=k(x+1),
|
上述方程中判别式△=9k2-6k+1=0,k=
| 1 |
| 3 |
又kAB=
| 1 |
| 3 |
所以AB与DE平行…(14分)
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,直线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.易错点是综合性强,难度大,容易出错.

练习册系列答案
相关题目
 17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|=
17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|= 如图,已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|等于( )
如图,已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|等于( ) 如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC.
如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC.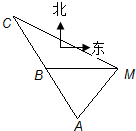 (2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )
(2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )