题目内容
 如图,已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|等于( )
如图,已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|等于( )分析:利用抛物线的定义和|AF|=|AB|+1就可得出|AB|=xA,同理可得:|CD|=xD,要分l⊥x轴和l不垂直x轴两种情况分别求值,当l⊥x轴时易求,当l不垂直x轴时,将直线的方程代入抛物线方程,利用根与系数关系可求得.
解答:解:∵y2=4x,焦点F(1,0),准线 l0:x=-1.
由定义得:|AF|=xA+1,
又∵|AF|=|AB|+1,∴|AB|=xA,
同理:|CD|=xD,
当l⊥x轴时,则xD=xA=1,∴|AB|•|CD|=1
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,
∴xAxD=1,∴|AB|•|CD|=1
综上所述,|AB|•|CD|=1
故选B.

由定义得:|AF|=xA+1,
又∵|AF|=|AB|+1,∴|AB|=xA,
同理:|CD|=xD,
当l⊥x轴时,则xD=xA=1,∴|AB|•|CD|=1
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,
∴xAxD=1,∴|AB|•|CD|=1
综上所述,|AB|•|CD|=1
故选B.
点评:本题主要考查抛物线的定义、一元二次方程的根与系数关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|=
17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|= 如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC.
如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC. 如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且
如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且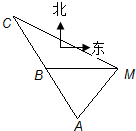 (2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )
(2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )