题目内容
2.若函数f(x)满足$f(x)+2f(\frac{1}{x})={log_2}x$,则f(2)的值( )| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
分析 由$f(x)+2f(\frac{1}{x})={log_2}x$,得$f(\frac{1}{x})+2f(x)=lo{g}_{2}\frac{1}{x}$,联立方程组求出f(x)=-log2x,由此能求出f(2)的值.
解答 解:∵$f(x)+2f(\frac{1}{x})={log_2}x$,①
∴$f(\frac{1}{x})+2f(x)=lo{g}_{2}\frac{1}{x}$,②
②×2-①,得:3f(x)=-3log2x,
解得f(x)=-log2x,
∴f(2)=-log22=-1.
故选:B.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
13.已知1<x<10,令a=lgx,b=log2(lgx),c=2lgx,则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | b<c<a |
10.在△ABC中,角A,B,C的对边分别为a,b,c,cos2$\frac{A}{2}$=$\frac{b+c}{2c}$,则△ABC的形状一定是( )
| A. | 正三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |
14.若f(x)=ax2+(2+a)x+1是偶函数,则f(x)的递增区间为( )
| A. | (-∞,0) | B. | [0,+∞) | C. | (-∞,+∞) | D. | [1,+∞) |
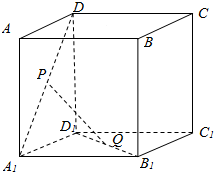 如图,正方体的棱长为a,P、Q分别为A1D、B1D1的中点
如图,正方体的棱长为a,P、Q分别为A1D、B1D1的中点