题目内容
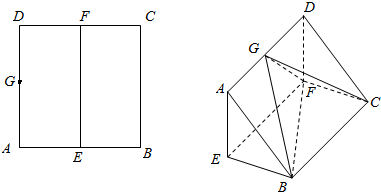
12.如图所示,正方形ABCD中,E、F、G分别是AB、CD、AD的中点,将ABCD沿EF折起,使FG⊥BG.(Ⅰ)证明:EB⊥平面AEFD;
(Ⅱ)求二面角G-BF-E的余弦值.
分析 (Ⅰ)设正方体的棱长为2,证明EF⊥面AEB.EB⊥AE,推出EB⊥面AEFB.
(Ⅱ)取EF的中点H,作HO⊥BF,垂足为O,连接GO,说明∠GOH就是所求二面角G-BF-E的平面角,在Rt△GHO中,求解二面角G-BF-E的余弦值.
解答  (Ⅰ)证明:设正方体的棱长为2,
(Ⅰ)证明:设正方体的棱长为2,
在Rt△BGF中,$GF=\sqrt{2},BF=\sqrt{5}$
所以$GB=\sqrt{3}$…(2分)
∵EF⊥AE,EF⊥EB,∴EF⊥面AEB.
∵AD∥EF,∴AD⊥面AEB,∴AD⊥AB
所以在Rt△BGF中,得$AB=\sqrt{2}$…(5分)
在△AEB中,又AE=BE=1∴EB⊥AE
又EF⊥EB∴EB⊥面AEFB…(7分)
(Ⅱ)解:取EF的中点H,则GH⊥EF,由(Ⅰ)知,EB⊥面AEFB,
所以面EFCB⊥面AEFB,所以GH⊥面EFCB,
作HO⊥BF,垂足为O,连接GO,由三垂线定理知,GO⊥BF,
所以∠GOH就是所求二面角G-BF-E的平面角.…(11分)
在Rt△GHO中,GH=1,$HO=\frac{1}{{\sqrt{5}}}$,
所以$GO=\frac{{\sqrt{6}}}{{\sqrt{5}}}$,所以$cos∠GOH=\frac{HO}{GO}=\frac{{\sqrt{6}}}{6}$
所以二面角G-BF-E的余弦值为$\frac{{\sqrt{6}}}{6}$.…(15分)
点评 本题考查直线与平面垂直的判断,二面角的平面角的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
2.若函数f(x)满足$f(x)+2f(\frac{1}{x})={log_2}x$,则f(2)的值( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
3.已知圆锥高为h,底面圆半径、锥高、母线长构成等比数列,则圆锥的侧面积是( )
| A. | $\frac{1}{3}π{h^2}$ | B. | $\frac{1}{2}π{h^2}$ | C. | πh2 | D. | 2πh2 |