题目内容
已知函数
(Ⅰ)若 在(0,
在(0, )单调递减,求a的最小值
)单调递减,求a的最小值
(Ⅱ)若 有两个极值点,求a的取值范围.
有两个极值点,求a的取值范围.
(Ⅰ)a的最小值为1; (Ⅱ)(0,1).
解析试题分析:(Ⅰ)将“f(x)在(0, )单调递减”转化为“"x∈(0,+∞),a≥
)单调递减”转化为“"x∈(0,+∞),a≥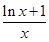 ”,然后才有构造函数的思想求解函数的最大值即可;(Ⅱ)通过对参数a 与1的讨论,借助求导的方法研究函数的单调性,进而分析保证有两个极值点的条件,通过解不等式求解求a的取值范围.
”,然后才有构造函数的思想求解函数的最大值即可;(Ⅱ)通过对参数a 与1的讨论,借助求导的方法研究函数的单调性,进而分析保证有两个极值点的条件,通过解不等式求解求a的取值范围.
试题解析:(Ⅰ)f¢(x)=lnx+1-ax.
f(x)单调递减当且仅当f¢(x)≤0,即"x∈(0,+∞),
a≥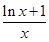 . ①
. ①
设g(x)=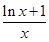 ,则g¢(x)=-
,则g¢(x)=-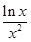 .
.
当x∈(0,1)时,g¢(x)>0,g(x)单调递增;
当x∈(1,+∞)时,g¢(x)<0,g(x)单调递减.
所以g(x)≤g(1)=1,故a的最小值为1. 5分
(Ⅱ)(1)由(Ⅰ)知,当a≥1时,f(x)没有极值点.
(2)当a≤0时,f¢(x)单调递增,f¢(x)至多有一个零点,f(x)不可能有两个极值点. 7分
(3)当0<a<1时,设h(x)=lnx+1-ax,则h¢(x)= -a.
-a.
当x∈(0, )时,h¢(x)>0,h(x)单调递增;
)时,h¢(x)>0,h(x)单调递增;
当x∈( ,+∞)时,h¢(x)<0,h(x)单调递减. 9分
,+∞)时,h¢(x)<0,h(x)单调递减. 9分
因为f¢( )=h(
)=h( )=ln
)=ln >0,f¢(
>0,f¢( )=h(
)=h( )=-
)=- <0,
<0,
所以f(x)在区间( ,
, )有一极小值点x1. 10分
)有一极小值点x1. 10分
由(Ⅰ)中的①式,有1≥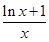 ,即lnx≤x-1,则ln
,即lnx≤x-1,则ln ≤
≤ -1,
-1,
故f¢(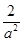 )=h(
)=h(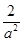 )=ln2+2ln
)=ln2+2ln +1-
+1-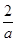 ≤ln2+2(
≤ln2+2( -1)+1-
-1)+1-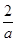 =ln2-1<0.
=ln2-1<0.
所以f(x)在区间( ,
,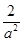 )有一极大值点x2.
)有一极大值点x2.
综上所述,a的取值范围是(0,1).
考点:1.函数的单调性、极值和最值;2.不等式恒成立.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案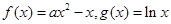 .
.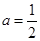 ,求函数
,求函数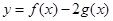 的极值,
的极值, ,使得
,使得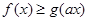 成立?若存在,求出实数
成立?若存在,求出实数 为实数,函数
为实数,函数
 的单调区间与极值;
的单调区间与极值; 且
且 时,
时,
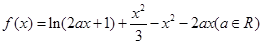
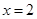 为
为 的极值点,求实数
的极值点,求实数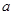 的值;
的值; 在
在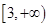 上为增函数,求实数
上为增函数,求实数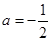 时,方程
时,方程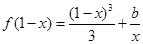 有实根,求实数
有实根,求实数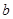 的最大值.
的最大值.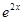 +2x+m,x∈R
+2x+m,x∈R +2mx+1.
+2mx+1.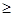 x2在(0,1 )上恒成立,求实数a的取值范围.
x2在(0,1 )上恒成立,求实数a的取值范围. .
. 的最小正周期
的最小正周期 ;
;
 ,
, ,
, ,以及
,以及 围成的平面图形的面积.
围成的平面图形的面积. 为函数
为函数 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线 的斜率
的斜率 .
. 在区间
在区间
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; .
. .
. 时,
时, ,求
,求 的最小值;
的最小值; 的通项
的通项 ,证明:
,证明: .
.