题目内容
设 为实数,函数
为实数,函数
(Ⅰ)求 的单调区间与极值;
的单调区间与极值;
(Ⅱ)求证:当 且
且 时,
时,
(Ⅰ) 的单调递减区间是
的单调递减区间是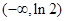 ,单调递增区间是
,单调递增区间是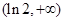 ,极小值为
,极小值为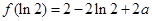 ;(Ⅱ) 见解析.
;(Ⅱ) 见解析.
解析试题分析:(Ⅰ)直接根据导数和零的大小关系求得单调区间,并由单调性求得极值;(Ⅱ)先由导数判断出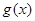 在R内单调递增,说明对任意
在R内单调递增,说明对任意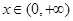 ,都有
,都有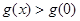 ,而
,而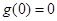 ,从而得证.
,从而得证.
试题解析:(1)解:由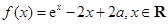 知,
知,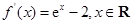 .
.
令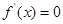 ,得
,得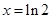 .于是,当
.于是,当 变化时,
变化时,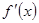 和
和 的变化情况如下表:
的变化情况如下表:
故
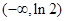
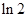
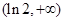
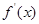
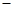
0 + 
单调递减 
单调递增  的单调递减区间是
的单调递减区间是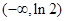 ,单调递增区间是
,单调递增区间是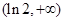 .
. 在
在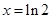 处取得极小值,极小值为
处取得极小值,极小值为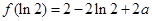 .
.
(2)证明:设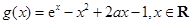 ,于是
,于是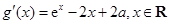 .
.
由(1)知,对任意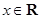 ,都有
,都有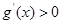 ,所以
,所以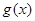 在R内单调递增.
在R内单调递增.
于是,当 时,对任意
时,对任意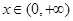 ,都有
,都有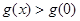 ,而
,而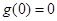 ,
,
从而对任意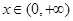 ,都有
,都有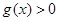 ,即
,即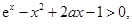 故
故
考点:1.利用导数研究函数的单调性;2. 利用导数求函数极值3.利用函数的最值证明不等式.

练习册系列答案
相关题目

 +ax-lnx(a∈R).
+ax-lnx(a∈R).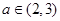 及任意
及任意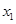 ,
, ∈[1,2],恒有
∈[1,2],恒有 成立,求实数m的取值范围.
成立,求实数m的取值范围.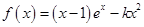 (其中
(其中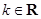 ).
).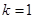 时,求函数
时,求函数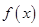 的单调区间和极值;
的单调区间和极值;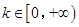 时,函数
时,函数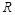 上有且只有一个零点.
上有且只有一个零点. .
. 的单调性;
的单调性; 的值,使不等式
的值,使不等式 恒成立.
恒成立.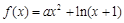 .
.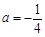 时,求函数
时,求函数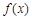 的单调区间;
的单调区间;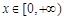 时,不等式
时,不等式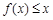 恒成立,求实数
恒成立,求实数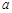 的取值范围.
的取值范围.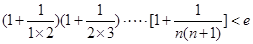 (
(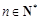 ,e是自然对数的底数).
,e是自然对数的底数).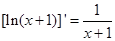
 排,在路南侧沿直线
排,在路南侧沿直线 排,现要在矩形区域
排,现要在矩形区域 内沿直线将
内沿直线将 ,
, ,公路两侧排管费用为每米1万元,穿过公路的
,公路两侧排管费用为每米1万元,穿过公路的 部分的排管费用为每米2万元,设
部分的排管费用为每米2万元,设 所成的小于
所成的小于 的角为
的角为 .
.
 关于
关于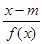 >
> 成立,求实数m的取值范围;
成立,求实数m的取值范围;
 在(0,
在(0, )单调递减,求a的最小值
)单调递减,求a的最小值  .
. 的极值,并证明:若
的极值,并证明:若 有
有 ;
;  ,且
,且 ,
, ,证明:
,证明: ,
, ,由上述结论猜想一个一般性结论(不需要证明);
,由上述结论猜想一个一般性结论(不需要证明); ,则
,则 .
.