题目内容
【题目】过点(0,2)的直线l与中心在原点,焦点在x轴上且离心率为 ![]() 的椭圆C相交于A、B两点,直线
的椭圆C相交于A、B两点,直线 ![]() 过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称.
过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称.
(1)求直线l的方程;
(2)求椭圆C的方程.
【答案】
(1)解:由e= ![]() =
= ![]() ,得
,得 ![]() ,从而a2=2b2,c=b,
,从而a2=2b2,c=b,
设椭圆方程为x2+2y2=2b2,A(x1,y1),B(x2,y2)在椭圆上,
则x12+2y12=2b2,x22+2y22=2b2,两式相减得,(x12﹣x22)+2(y12﹣y22)=0,
![]() =﹣
=﹣ ![]()
设AB中点为(x0,y0),则kAB=﹣ ![]()
又(x0,y0),在直线 ![]() 上,
上, ![]() ,于是:
,于是:
kAB=﹣ ![]() =﹣1,则直线l的方程为y=﹣x+2
=﹣1,则直线l的方程为y=﹣x+2
(2)解:右焦点(b,0)关于直线l的对称点设为:(x′,y′),
则 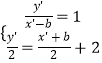 解得
解得 ![]() ,
,
由点(2,2﹣b)在椭圆上,得4+2(2﹣b)2=2b2,b2= ![]() ,a2=
,a2= ![]() ,
,
∴所求椭圆C的方程的方程为: ![]()
【解析】本题求直线l的方程关键在于求直线的斜率,根据题意设出椭圆方程,并设出点A,B及线段AB中点的坐标,利用点A,B在椭圆上得到用线段AB中点坐标表示的直线l的斜率,结合该中点在直线![]() 上即可求得直线l的斜率;(2)椭圆C上存在一点与右焦点关于直线l对称,那么右焦点与其对称点所在的直线与直线l互相垂直即两直线斜率积为-1,而且右焦点与其对称点组成的线段的中点在直线l上.
上即可求得直线l的斜率;(2)椭圆C上存在一点与右焦点关于直线l对称,那么右焦点与其对称点所在的直线与直线l互相垂直即两直线斜率积为-1,而且右焦点与其对称点组成的线段的中点在直线l上.
【考点精析】掌握椭圆的标准方程是解答本题的根本,需要知道椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

【题目】为了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位三十岁到四十岁的公务员,得到如下列联表,因不慎丢失部分数据.
(1)完成表格数据,判断是否有99%以上的把握认为“生二胎意愿与性别有关”并说明理由;
(2)已知15位有意愿生二胎的女性公务员中有两位来自省妇联,该部门打算从这15位有意愿生二胎的女性公务员中随机邀请两位来参加座谈,设邀请的2人中来自省妇联的人数为X,求X的分布列及数学期望E(X).
男性公务员 | 女性公务员 | 总计 | |
有意愿生二胎 | 15 | 45 | |
无意愿生二胎 | 25 | ||
总计 |
P(k2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
附: ![]() .
.