Question

【题目】如图，四边形ABCD是梯形，四边形CDEF是矩形，且平面ABCD⊥平面CDEF，∠BAD=∠CDA=90°，AB=AD=DE= CD=2，M是线段AE上的动点．
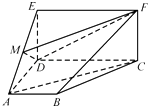
（Ⅰ）试确定点M的位置，使AC∥平面MDF，并说明理由；
（Ⅱ）在（Ⅰ）的条件下，求平面MDF将几何体ADE﹣BCF分成的两部分的体积之比．

Answer 1

【答案】解：（Ⅰ）当M是线段AE的中点时，AC∥平面MDF．证明如下：

连结CE，交DF于N，连结MN，

由于M、N分别是AE、CE的中点，所以MN∥AC，

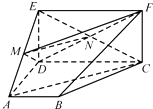
由于MN平面MDF，又AC平面MDF，

所以AC∥平面MDF．

（Ⅱ）如图，将几何体ADE﹣BCF补成三棱柱ADE﹣B′CF，

三棱柱ADE﹣B′CF的体积为 ，

则几何体ADE﹣BCF的体积

VADE﹣BCF=V三棱柱ADE﹣BCF﹣VF﹣BB'C= ．

三棱锥F﹣DEM的体积V三棱锥M﹣DEF= ，

故两部分的体积之比为 （答1：4，4，4：1均可）

【解析】（Ⅰ）首先，根据所给图形，得到当M是线段AE的中点时，AC∥平面MDF．然后，根据线面平行的判定定理进行证明即可；（Ⅱ）利用补图法，将几何体ADE﹣BCF补成三棱柱ADE﹣B′CF，然后，借助于柱体和椎体的体积公式进行求解即可．
【考点精析】根据题目的已知条件，利用直线与平面平行的判定和直线与平面垂直的判定的相关知识可以得到问题的答案，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．