题目内容
8.已知数列{an}中,a1=t(t为非负常数),数列{an}的前n项和为Sn,且Sn满足Sn+1=3Sn(Ⅰ)当t=1时,求数列{an}的通项公式;
(Ⅱ)若bn=nan,求数列{bn}的前n项和Tn.
分析 (I)由Sn+1=3Sn,可知数列{Sn}是首项为1,公比为3的等比数列,即可得出Sn.当n≥2时,利用an=Sn-Sn-1即可得出.
(II)由(I)可得:bn=$\left\{\begin{array}{l}{t,n=1}\\{2nt•{3}^{n-2},n≥2}\end{array}\right.$.当n=1时,T1=t.当n≥2时,Tn=t+2t(2+3×3+4×32+…+n•3n-2),再利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 解:(I)由Sn+1=3Sn,可知数列{Sn}是首项为1,公比为3的等比数列,
∴Sn=3n-1.
当n≥2时,an=Sn-Sn-1=3n-1-3n-2=2×3n-2.
∴an=$\left\{\begin{array}{l}{1,n=1}\\{2×{3}^{n-2},n≥2}\end{array}\right.$.
(II)由(I)可得:bn=$\left\{\begin{array}{l}{t,n=1}\\{2nt•{3}^{n-2},n≥2}\end{array}\right.$.
∴当n=1时,T1=t.
当n≥2时,Tn=t+2t(2+3×3+4×32+…+n•3n-2),
3Tn=3t+2t[2×3+3×32+…+(n-1)•3n-2+n•3n-1],
∴-2Tn=-2t+2t(2+3+32+…+3n-2-n•3n-1)=-2t+2t$(1+\frac{{3}^{n-1}-1}{3-1}-n×{3}^{n-1})$=t(1-2n)•3n-1-t,
∴Tn=$\frac{(2n-1)t•{3}^{n-1}+t}{2}$.
当t=1时,上式也成立.
∴Tn=$\frac{(2n-1)t•{3}^{n-1}+t}{2}$.
点评 本题考查了“错位相减法”、等比数列的通项公式及其前n项和公式,考查了分类讨论方法、推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 2$\sqrt{2}$ | B. | 4 | C. | 6 | D. | 10 |
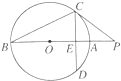 如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,若圆O的半径为2,PA=1,求PC•CE的值.
如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,若圆O的半径为2,PA=1,求PC•CE的值.