Question

【题目】已知四条直线两两相交，且不共点，求证：这四条直线在同一平面内．

Answer 1

【答案】证明见解析

【解析】

四条直线两两相交包括：四条直线中有三条相交于一点与四条直线中任何三条都不共点两种情况．
无论哪种情况先由两直线相交确定一个平面，再通过直线上两点在一个平面内则该直线在这个平面内，即可证明．

已知：a，b，c，d四条直线两两相交，且不共点，求证：a，b，c，d四线共面．

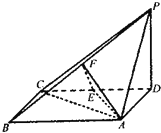
证明：（1）若a，b，c三线共点于O，

如图所示，，

经过d与点O有且只有一个平面α．

，B，C分别是d与a，b，c的交点，

，B，C三点在平面α内．由公理1知a，b，c都在平面α内，故a，b，c，d共面．

（2）若a，b，c，d无三线共点，

如图所示，，

经过a，b有且仅有一个平面α，

，．由公理1知．

同理，，从而有a，b，c，d共面．

综上所述：四条直线两两相交，且不共点，这四条直线在同一平面内．