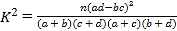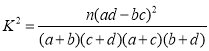题目内容
【题目】已知点![]() 与两个定点
与两个定点![]() 距离的比是一个正数
距离的比是一个正数![]() .
.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)当![]() 时得曲线
时得曲线![]() 的方程,把曲线
的方程,把曲线![]() 向左平移三个单位长度得到曲线
向左平移三个单位长度得到曲线![]() ,已知点
,已知点![]() ,
,![]() ,点
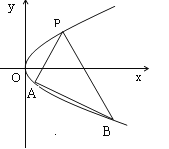
,点![]() 是曲线
是曲线![]() 上任意一点,求
上任意一点,求![]() 的最小值;
的最小值;
(3)若直线![]() 与曲线
与曲线![]() 交于C、D两点,点
交于C、D两点,点![]() 是x轴上的点,使得
是x轴上的点,使得![]() 恒为定值,求点P的坐标和定值.
恒为定值,求点P的坐标和定值.
【答案】(1)当![]() 时,
时,![]() ,此时轨迹为
,此时轨迹为![]() 轴所在的直线;
轴所在的直线;
当![]() 时,可得:
时,可得:![]() ,此时轨迹为以
,此时轨迹为以![]() 为圆心,
为圆心,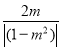 为半径的圆;
为半径的圆;
(2)![]() ;(3)点P的坐标
;(3)点P的坐标![]() ,定值为
,定值为![]() .
.
【解析】
(1)由题意得: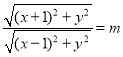 , 对其化简,分
, 对其化简,分![]() 与
与![]() 进行讨论可得答案;
进行讨论可得答案;
(2)代入![]() 可得曲线
可得曲线![]() 的方程,由题意可得曲线
的方程,由题意可得曲线![]() 的方程,点
的方程,点![]() 的坐标为
的坐标为![]() ,可得
,可得![]() 与
与![]() ,由平面向量和三角函数知识,可得
,由平面向量和三角函数知识,可得![]() 的最小值;
的最小值;
(3)设C、D两点坐标![]() ,
,![]() ,即
,即![]() ,
,![]() ,联立直线与圆,
,联立直线与圆,![]() 用
用![]() 与
与![]() 表示,由
表示,由![]() 恒为定值,可得
恒为定值,可得![]() 的值,可得答案.
的值,可得答案.
解:(1)由题意得: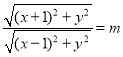 ,
,
化简可得:![]() ,
,
当![]() 时,
时,![]() ,此时轨迹为
,此时轨迹为![]() 轴所在的直线;
轴所在的直线;
当![]() 时,可得:
时,可得:![]() ,
,
此时轨迹为以![]() 为圆心,
为圆心,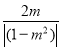 为半径的圆;
为半径的圆;
(2)![]() 时,可得曲线
时,可得曲线![]() 的方程为:
的方程为:![]() ,
,
由曲线![]() 向左平移三个单位长度得到曲线
向左平移三个单位长度得到曲线![]() ,可得
,可得![]() 的方程为:
的方程为:![]() ,
,
点![]() 的坐标为
的坐标为![]() ,由点
,由点![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,
故可得:![]()
![]()
![]() ,其中
,其中![]() ,
,
可得![]() 的最小值为:
的最小值为:![]() ;
;
(3)由(2)可得曲线![]() 的方程为:
的方程为:![]() ,
,
由直线![]() 与曲线
与曲线![]() 交于C、D两点,设C、D两点坐标
交于C、D两点,设C、D两点坐标![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
联立直线![]() 与圆
与圆![]() ,可得
,可得![]()
可得:![]() ,
,![]() ,
,
由点![]() ,可得
,可得![]() ,
,![]() ,
,
可得:![]() ,
,
可得![]() ,
,
由![]() 恒为定值,故
恒为定值,故![]() 与
与![]() 的值无关,故可得
的值无关,故可得![]()
点P的坐标![]() ,定值为
,定值为![]() .
.

练习册系列答案
相关题目