题目内容
【题目】已知函数f(x)=![]() +
+![]() .
.
(1)当m=0时,求不等式f(x)≤9的解集;
(2)当m=2时,若x∈(1,4),f(x) ![]() 2x
2x![]() a<0,求a的取值范围.
a<0,求a的取值范围.
【答案】(1) {x|![]()
![]() ≤x≤
≤x≤![]() }. (2) a∈[3,+∞).
}. (2) a∈[3,+∞).
【解析】
(1) 对![]() 分三种情况讨论,分别去掉绝对值符号,然后求解不等式组,再求并集即可得结果;(2)原不等式等价于
分三种情况讨论,分别去掉绝对值符号,然后求解不等式组,再求并集即可得结果;(2)原不等式等价于![]() x+2
x+2![]() a<2x
a<2x![]() 4<x
4<x![]() 2+a,得
2+a,得![]() <x<a+2,可得(1,4)(
<x<a+2,可得(1,4)(![]() ,a+2), 根据包含关系列不等式求解即可.
,a+2), 根据包含关系列不等式求解即可.
(1)f(x)=|2x![]() 4|+|x|≤9,
4|+|x|≤9,
即![]() 或
或![]() 或
或![]()
得2<x≤![]() 或0≤x≤2或
或0≤x≤2或![]()
![]() ≤x<0.
≤x<0.
所以f(x)≤9的解集为{x|![]()
![]() ≤x≤
≤x≤![]() }.
}.
(2)当m=2时,f(x) ![]() 2x
2x![]() a<0对x∈(1,4)恒成立,
a<0对x∈(1,4)恒成立,
等价于![]() <x
<x![]() 2+a,x∈(1,4)恒成立.
2+a,x∈(1,4)恒成立.
由![]() x+2
x+2![]() a<2x
a<2x![]() 4<x
4<x![]() 2+a,得
2+a,得![]() <x<a+2,
<x<a+2,
由题意得(1,4)(![]() ,a+2),
,a+2),
所以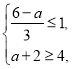 解得a≥3,即a∈[3,+∞).
解得a≥3,即a∈[3,+∞).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】海关对同时从![]() 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
地区 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.