题目内容
【题目】已知直线![]() 与抛物线
与抛物线![]() 相切,且与
相切,且与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() .若动点
.若动点![]() 与两定点
与两定点![]() 所构成三角形的周长为6.
所构成三角形的周长为6.
(Ⅰ) 求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ) 设斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,当
两点,当![]() ,且
,且![]() 位于直线
位于直线![]() 的两侧时,证明:
的两侧时,证明: ![]() .
.
【答案】(Ⅰ) ![]() (
(![]() );(Ⅱ)见解析.
);(Ⅱ)见解析.
【解析】试题分析:(Ⅰ先由判别式为零可得![]() 的值,再根据三角形周长可得
的值,再根据三角形周长可得![]() 进而由椭圆定义可得方程;(Ⅱ)设直线
进而由椭圆定义可得方程;(Ⅱ)设直线![]() 方程
方程![]() ,联立
,联立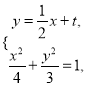 得
得![]() ,根据直线斜率公式及韦达定理利用分析法证明
,根据直线斜率公式及韦达定理利用分析法证明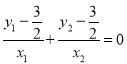 即可.
即可.
试题解析:(Ⅰ) 因为直线![]() 与抛物线
与抛物线![]() 相切,所以方程
相切,所以方程![]() 有等根,
有等根,
则![]() ,即
,即![]() ,所以
,所以![]() .
.
又因为动点![]() 与定点
与定点![]() 所构成的三角形周长为6,且
所构成的三角形周长为6,且![]() ,
,
所以![]()
根据椭圆的定义,动点![]() 在以
在以![]() 为焦点的椭圆上,且不在
为焦点的椭圆上,且不在![]() 轴上,
轴上,
所以![]() ,得
,得![]() ,则
,则![]() ,
,
即曲线![]() 的方程为
的方程为![]() (
(![]() ).
).
(Ⅱ)设直线![]() 方程
方程![]()
![]() ,联立
,联立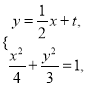 得
得![]() ,
,
△=-3![]() +12>0,所以
+12>0,所以![]() , 此时直线
, 此时直线![]() 与曲线
与曲线![]() 有两个交点
有两个交点![]() ,
, ![]() ,
,
设![]()
![]() ,
, ![]()
![]() ,则
,则![]() ,
, ![]()
∵![]() ,不妨取
,不妨取![]() ,
,
要证明![]() 恒成立,即证明
恒成立,即证明![]() ,
,
即证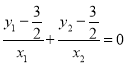 ,也就是要证
,也就是要证![]()
即证![]() 由韦达定理所得结论可得此式子显然成立,
由韦达定理所得结论可得此式子显然成立,
所以![]() 成立.
成立.

练习册系列答案
相关题目