题目内容
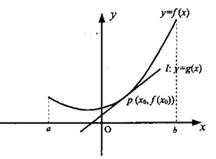
设a∈R,函数f(x)=x3+ax2+(a-3)x的导函数是 f ’(x),若f ’( x )是偶函数,则曲线
y=f (x) 在原点处的切线方程为 ( )
y=f (x) 在原点处的切线方程为 ( )
| A.y=-3x | B.y=-2x | C.y=3x | D.y=2x |
A
本题考查导数的运算和几何意义,偶函数概念.
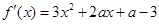 ,因为
,因为 是偶函数,所以
是偶函数,所以
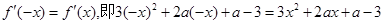 对任意
对任意 恒成立,整理得
恒成立,整理得 对任意
对任意 恒成立,所以
恒成立,所以 于是
于是 曲线
曲线 在原点处的切线斜率为
在原点处的切线斜率为 则曲线
则曲线 在原点处的切线方程为
在原点处的切线方程为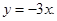 故选A
故选A
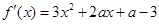 ,因为
,因为 是偶函数,所以
是偶函数,所以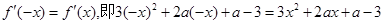 对任意
对任意 恒成立,整理得
恒成立,整理得 对任意
对任意 恒成立,所以
恒成立,所以 于是
于是 曲线
曲线 在原点处的切线斜率为
在原点处的切线斜率为 则曲线
则曲线 在原点处的切线方程为
在原点处的切线方程为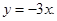 故选A
故选A
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
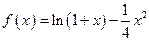 ;
;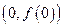 处的切线方程;
处的切线方程;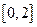 上的最大值和最小值.
上的最大值和最小值.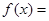
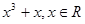 ,当0
,当0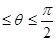 时,
时,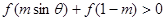 恒成立,则实数
恒成立,则实数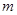 的取值范围是 ( )
的取值范围是 ( )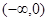
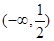
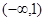
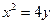 上一点P到定点A(0,1)的距离为2,则点P到x轴的距离为
上一点P到定点A(0,1)的距离为2,则点P到x轴的距离为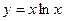 的单调递减区间是(
的单调递减区间是( )
)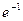 ,+∞)
,+∞)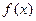 =
=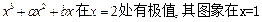 处的
处的 切线平行于直线
切线平行于直线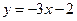 ,试求函数
,试求函数
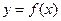 的对称轴为
的对称轴为 ,当
,当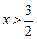 时
时 , 则
, 则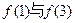 的大小关系为( )
的大小关系为( )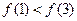
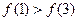
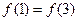

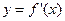 是函数
是函数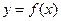 的导函数,且函数
的导函数,且函数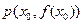 处的切线为
处的切线为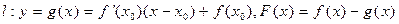 ,如果函数
,如果函数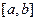 上的图像如图所示,且
上的图像如图所示,且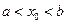 ,那么 ( )
,那么 ( )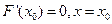 是
是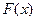 的极大值
的极大值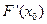 =
=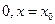 是
是 不是
不是